Ctrl+K

Bottleneck distance user manual#

Definition#

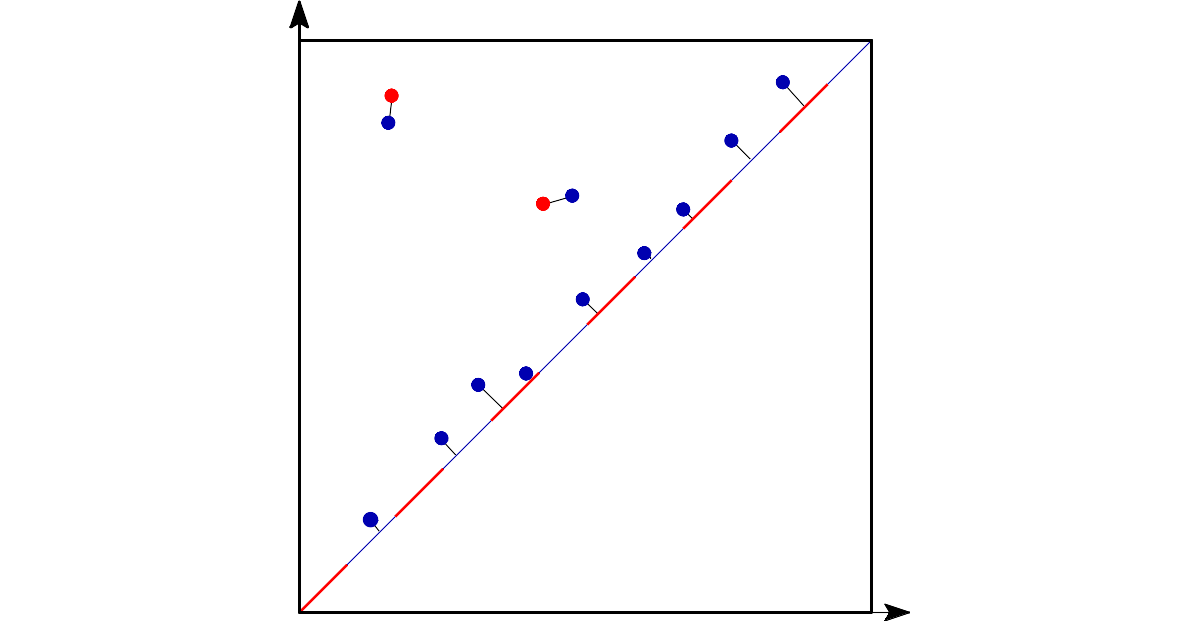
_images/perturb_pd.png

Bottleneck distance is the length of the longest edge#

Bottleneck distance measures the similarity between two persistence diagrams. It’s the shortest distance b for which there exists a perfect matching between the points of the two diagrams (+ all the diagonal points) such that any couple of matched points are at distance at most b, where the distance between points is the sup norm in \(\mathbb{R}^2\).
Author:

François Godi

Since:

GUDHI 2.0.0

License:

MIT (GPL v3)

Requires:

CGAL

This implementation by François Godi is based on ideas from “Geometry Helps in Bottleneck Matching and Related Problems” [21] and requires CGAL (GPL v3).

gudhi.bottleneck_distance(diagram_1: numpy.ndarray[numpy.float64], diagram_2: numpy.ndarray[numpy.float64], e: float | None = None) → float#

Compute the Bottleneck distance between two diagrams. Points at infinity and on the diagonal are supported.

Parameters:

  • diagram_1 (numpy array of shape (m,2)) – The first diagram.

  • diagram_2 (numpy array of shape (n,2)) – The second diagram.

  • e (float) – If e is 0, this uses an expensive algorithm to compute the exact distance. If e is not 0, it asks for an additive e-approximation, and currently also allows a small multiplicative error (the last 2 or 3 bits of the mantissa may be wrong). This version of the algorithm takes advantage of the limited precision of double and is usually a lot faster to compute, whatever the value of e. Thus, by default (e=None), e is the smallest positive double.

Return type:

float

Returns:

the bottleneck distance.

This other implementation comes from Hera (BSD-3-Clause) which is based on “Geometry Helps to Compare Persistence Diagrams” [24] by Michael Kerber, Dmitriy Morozov, and Arnur Nigmetov.

Warning

Beware that its approximation allows for a multiplicative error, while the function above uses an additive error.

gudhi.hera.bottleneck_distance(X: numpy.ndarray[numpy.float64], Y: numpy.ndarray[numpy.float64], delta: float = 0.01) → float#

Compute the Bottleneck distance between two diagrams. Points at infinity are supported.

Note

Points on the diagonal are not supported and must be filtered out before calling this function.

Parameters:

  • X (n x 2 numpy array) – First diagram

  • Y (n x 2 numpy array) – Second diagram

  • delta (float) – Relative error 1+delta

Returns:

(approximate) bottleneck distance d_B(X,Y)

Return type:

float

Distance computation#

The following example explains how the distance is computed:

import gudhi

message = "Bottleneck distance = " + '%.1f' % gudhi.bottleneck_distance([[0., 0.]], [[0., 13.]])
print(message)

Bottleneck distance = 6.5
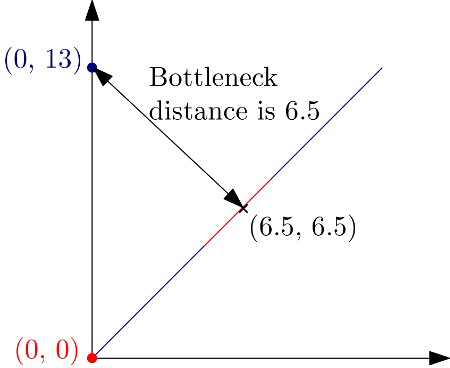
_images/bottleneck_distance_example.png

The point (0, 13) is at distance 6.5 from the diagonal and more specifically from the point (6.5, 6.5).#

Basic example#

This other example computes the bottleneck distance from 2 persistence diagrams:

import gudhi

diag1 = [[2.7, 3.7],[9.6, 14.],[34.2, 34.974], [3.,float('Inf')]]
diag2 = [[2.8, 4.45],[9.5, 14.1],[3.2,float('Inf')]]

message = "Bottleneck distance approximation = " + '%.2f' % gudhi.bottleneck_distance(diag1, diag2, 0.1)
print(message)

message = "Bottleneck distance value = " + '%.2f' % gudhi.bottleneck_distance(diag1, diag2)
print(message)

The output is:

Bottleneck distance approximation = 0.72
Bottleneck distance value = 0.75
On this page