Bottleneck distance user manual¶
Definition¶
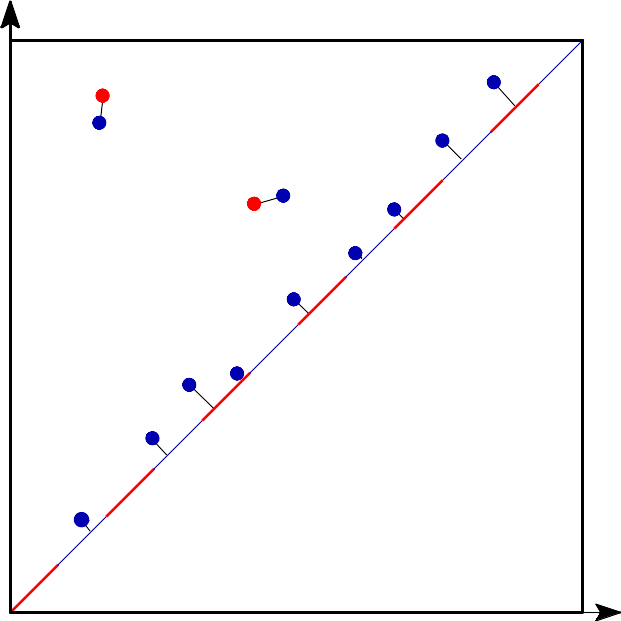
Bottleneck distance is the length of the longest edge¶ |
Bottleneck distance measures the similarity between two persistence diagrams. It’s the shortest distance b for which there exists a perfect matching between the points of the two diagrams (+ all the diagonal points) such that any couple of matched points are at distance at most b, where the distance between points is the sup norm in \(\mathbb{R}^2\). |
|
This implementation is based on ideas from “Geometry Helps in Bottleneck Matching and Related Problems” [1]. Another relevant publication, although it was not used is “Geometry Helps to Compare Persistence Diagrams” [2].
Function¶
-
gudhi.bottleneck_distance()¶ This function returns the point corresponding to a given vertex.
- Parameters
diagram_1¶ (vector[pair[double, double]]) – The first diagram.
diagram_2¶ (vector[pair[double, double]]) – The second diagram.
e¶ (float) –
If e is 0, this uses an expensive algorithm to compute the exact distance. If e is not 0, it asks for an additive e-approximation, and currently also allows a small multiplicative error (the last 2 or 3 bits of the mantissa may be wrong). This version of the algorithm takes advantage of the limited precision of double and is usually a lot faster to compute, whatever the value of e.
Thus, by default, e is the smallest positive double.
- Return type
float
- Returns
the bottleneck distance.
Distance computation¶
The following example explains how the distance is computed:
import gudhi
message = "Bottleneck distance = " + '%.1f' % gudhi.bottleneck_distance([[0., 0.]], [[0., 13.]])
print(message)
Bottleneck distance = 6.5
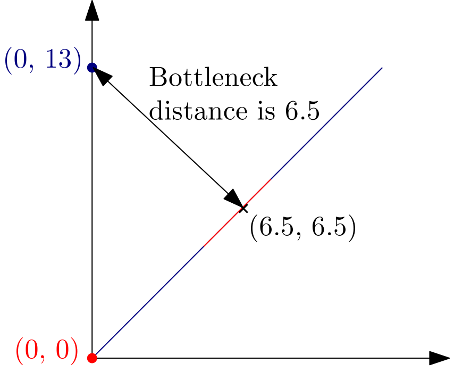
The point (0, 13) is at distance 6.5 from the diagonal and more specifically from the point (6.5, 6.5)¶
Basic example¶
This other example computes the bottleneck distance from 2 persistence diagrams:
import gudhi
diag1 = [[2.7, 3.7],[9.6, 14.],[34.2, 34.974], [3.,float('Inf')]]
diag2 = [[2.8, 4.45],[9.5, 14.1],[3.2,float('Inf')]]
message = "Bottleneck distance approximation = " + '%.2f' % gudhi.bottleneck_distance(diag1, diag2, 0.1)
print(message)
message = "Bottleneck distance value = " + '%.2f' % gudhi.bottleneck_distance(diag1, diag2)
print(message)
The output is:
Bottleneck distance approximation = 0.81
Bottleneck distance value = 0.75