Alpha complex user manual#
Definition#
|
Alpha complex is a simplicial complex constructed from the finite cells of a Delaunay Triangulation. It has the same persistent homology as the Čech complex and is significantly smaller. |
|
AlphaComplex is constructing a SimplexTree using
Delaunay Triangulation
[17] from the Computational Geometry Algorithms Library
[32].
Remarks#
When an \(\alpha\)-complex is constructed with an infinite value of \(\alpha^2\), the complex is a Delaunay complex (with special filtration values). The Delaunay complex without filtration values is also available by passing
default_filtration_value = Truetocreate_simplex_tree().For people only interested in the topology of the Alpha complex (for instance persistence), Alpha complex is equivalent to the Čech complex and much smaller if you do not bound the radii. Čech complex can still make sense in higher dimension precisely because you can bound the radii.
Using the default
precision = 'safe'makes the construction safe. If you passprecision = 'exact'to__init__(), the filtration values are the exact ones converted to float. This can be very slow. If you passprecision = 'safe'(the default), the filtration values are only guaranteed to have a small multiplicative error compared to the exact value, seeset_float_relative_precision()to modify the precision. A drawback, when computing persistence, is that an empty exact interval [10^12,10^12] may become a non-empty approximate interval [10^12,10^12+10^6]. Usingprecision = 'fast'makes the computations slightly faster, and the combinatorics are still exact, but the computation of filtration values can exceptionally be arbitrarily bad. In all cases, we still guarantee that the output is a valid filtration (faces have a filtration value no larger than their cofaces).
Example from points#
This example builds the alpha-complex from the given points:
from gudhi import AlphaComplex
ac = AlphaComplex(points=[[1, 1], [7, 0], [4, 6], [9, 6], [0, 14], [2, 19], [9, 17]])
stree = ac.create_simplex_tree()
print('Alpha complex is of dimension ', stree.dimension(), ' - ',
stree.num_simplices(), ' simplices - ', stree.num_vertices(), ' vertices.')
fmt = '%s -> %.2f'
for filtered_value in stree.get_filtration():
print(fmt % tuple(filtered_value))
The output is:
Alpha complex is of dimension 2 - 25 simplices - 7 vertices.
[0] -> 0.00
[1] -> 0.00
[2] -> 0.00
[3] -> 0.00
[4] -> 0.00
[5] -> 0.00
[6] -> 0.00
[2, 3] -> 6.25
[4, 5] -> 7.25
[0, 2] -> 8.50
[0, 1] -> 9.25
[1, 3] -> 10.00
[1, 2] -> 11.25
[1, 2, 3] -> 12.50
[0, 1, 2] -> 13.00
[5, 6] -> 13.25
[2, 4] -> 20.00
[4, 6] -> 22.74
[4, 5, 6] -> 22.74
[3, 6] -> 30.25
[2, 6] -> 36.50
[2, 3, 6] -> 36.50
[2, 4, 6] -> 37.24
[0, 4] -> 59.71
[0, 2, 4] -> 59.71
Algorithm#
Data structure#
In order to build the alpha complex, first, a Simplex tree is built from the cells of a Delaunay Triangulation. (The filtration value is set to NaN, which stands for unknown value):
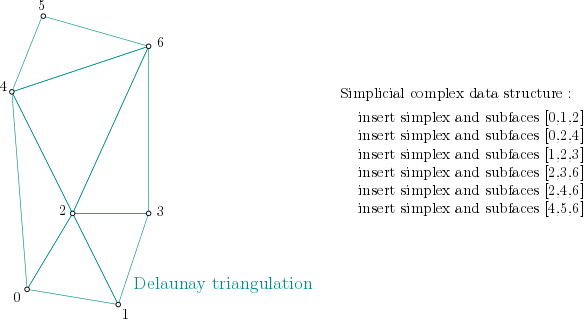
Simplex tree structure construction example#
Filtration value computation algorithm#
for i : dimension → 0 do
for all σ of dimension i
if filtration(σ) is NaN then
filtration(σ) = α²(σ)
end if
for all τ face of σ do // propagate alpha filtration value
if filtration(τ) is not NaN then
filtration(τ) = min( filtration(τ), filtration(σ) )
else
if τ is not Gabriel for σ then
filtration(τ) = filtration(σ)
end if
end if
end for
end for
end for
make_filtration_non_decreasing()
prune_above_filtration()
Dimension 2#
From the example above, it means the algorithm looks into each triangle ([0,1,2], [0,2,4], [1,2,3], …), computes the filtration value of the triangle, and then propagates the filtration value as described here:
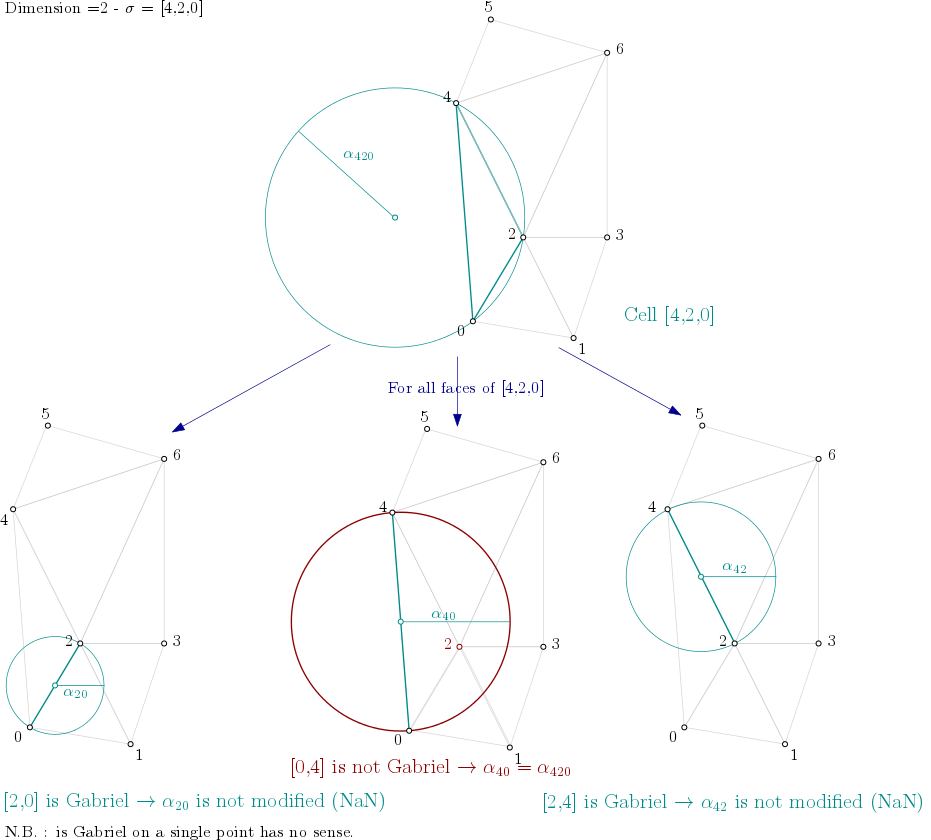
Filtration value propagation example#
Dimension 1#
Then, the algorithm looks into each edge ([0,1], [0,2], [1,2], …), computes the filtration value of the edge (in this case, propagation will have no effect).
Dimension 0#
Finally, the algorithm looks into each vertex ([0], [1], [2], [3], [4], [5] and [6]) and sets the filtration value (0 in case of a vertex - propagation will have no effect).
Non decreasing filtration values#
As the squared radii computed by CGAL are an approximation, it might happen that these
\(\alpha^2\) values do not quite define a proper filtration (i.e. non-decreasing with
respect to inclusion).
We fix that up by calling make_filtration_non_decreasing() (cf.
C++ version).
Note
This is not the case in exact version, this is the reason why it is not called in this case.
Prune above given filtration value#
The simplex tree is pruned from the given maximum \(\alpha^2\) value (cf.
prune_above_filtration()). Note that this does not provide any kind
of speed-up, since we always first build the full filtered complex, so it is recommended not to use
max_alpha_square.
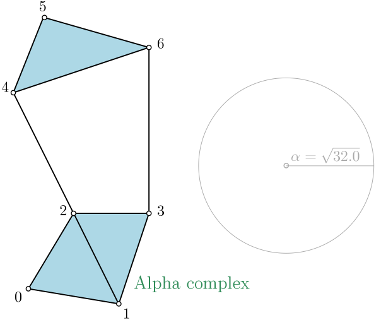
In the following example, a threshold of \(\alpha^2 = 32.0\) is used.
Weighted version#
A weighted version for Alpha complex is available. It is like a usual Alpha complex, but based on a CGAL regular triangulation.
This example builds the weighted alpha-complex of a small molecule, where atoms have different sizes. It is taken from CGAL 3d weighted alpha shapes.
Then, it is asked to display information about the alpha complex.
from gudhi import AlphaComplex
wgt_ac = AlphaComplex(points=[[ 1., -1., -1.],
[-1., 1., -1.],
[-1., -1., 1.],
[ 1., 1., 1.],
[ 2., 2., 2.]],
weights = [4., 4., 4., 4., 1.])
stree = wgt_ac.create_simplex_tree()
print('Weighted alpha complex is of dimension ', stree.dimension(), ' - ',
stree.num_simplices(), ' simplices - ', stree.num_vertices(), ' vertices.')
fmt = '%s -> %.2f'
for simplex in stree.get_simplices():
print(fmt % tuple(simplex))
The output is:
Weighted alpha complex is of dimension 3 - 29 simplices - 5 vertices.
[0, 1, 2, 3] -> -1.00
[0, 1, 2] -> -1.33
[0, 1, 3, 4] -> 95.00
[0, 1, 3] -> -1.33
[0, 1, 4] -> 95.00
[0, 1] -> -2.00
[0, 2, 3, 4] -> 95.00
[0, 2, 3] -> -1.33
[0, 2, 4] -> 95.00
[0, 2] -> -2.00
[0, 3, 4] -> 23.00
[0, 3] -> -2.00
[0, 4] -> 23.00
[0] -> -4.00
[1, 2, 3, 4] -> 95.00
[1, 2, 3] -> -1.33
[1, 2, 4] -> 95.00
[1, 2] -> -2.00
[1, 3, 4] -> 23.00
[1, 3] -> -2.00
[1, 4] -> 23.00
[1] -> -4.00
[2, 3, 4] -> 23.00
[2, 3] -> -2.00
[2, 4] -> 23.00
[2] -> -4.00
[3, 4] -> -1.00
[3] -> -4.00
[4] -> -1.00
Example from OFF file#
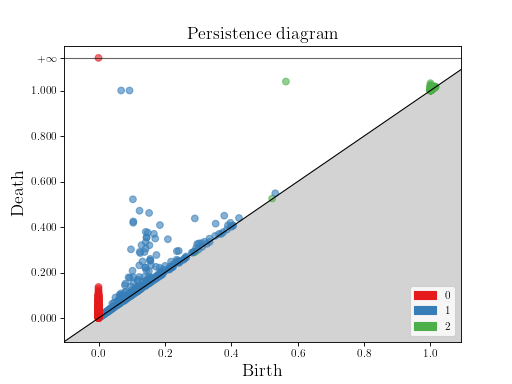
This example builds the alpha complex from 300 random points on a 2-torus, given by an OFF file.
Then, it computes the persistence diagram and displays it:
import matplotlib.pyplot as plt
import gudhi as gd
off_file = gd.__root_source_dir__ + '/data/points/tore3D_300.off'
points = gd.read_points_from_off_file(off_file = off_file)
stree = gd.AlphaComplex(points = points).create_simplex_tree()
dgm = stree.persistence()
gd.plot_persistence_diagram(dgm, legend = True)
plt.show()
(Source code, png, hires.png, pdf)