Čech complex

Classes
class	Gudhi::cech_complex::Cech_complex< Kernel, SimplicialComplexForCechComplex >
	Cech complex class. More...

Functions
template<bool Output_squared_values = true, typename Kernel , typename SimplicialComplexForMEB , typename PointRange >
void	Gudhi::cech_complex::assign_MEB_filtration (Kernel &&k, SimplicialComplexForMEB &complex, PointRange const &points, bool exact=false)
	Given a simplicial complex and an embedding of its vertices, this assigns to each simplex a filtration value equal to the squared (or not squared in function of Output_squared_values) radius of its minimal enclosing ball (MEB). More...

Detailed Description

Author

Vincent Rouvreau, Hind Montassif, Marc Glisse

Čech complex definition

Čech complex (Wikipedia) is a simplicial complex constructed from a proximity graph. The set of all simplices is filtered by the radius of their minimal enclosing ball.

The input shall be a range of points where a point is defined as CGAL kernel Point_d.

Remarks

For people only interested in the topology of the Čech complex (for instance persistence), Alpha complex is equivalent to the Čech complex and much smaller if you do not bound the radii. Čech complex can still make sense in higher dimension precisely because you can bound the radii.

Algorithm

Cech_complex first builds a proximity graph from a point cloud. The filtration value of each edge of the Gudhi::Proximity_graph is computed using CGAL kernel functions.

All edges that have a filtration value strictly greater than a user given maximal radius value, \(max\_radius\), are not inserted into the complex.

Vertex name correspond to the index of the point in the given range (aka. the point cloud).

Čech complex proximity graph representation

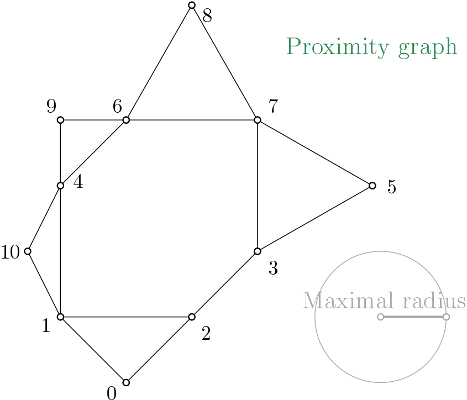
When creating a simplicial complex from this proximity graph, Cech_complex inserts the proximity graph into the simplicial complex data structure, and then expands the simplicial complex when required.

On this example, as edges \((x,y)\), \((y,z)\) and \((z,y)\) are in the complex, the minimal ball radius containing the points \((x,y,z)\) is computed.

\((x,y,z)\) is inserted to the simplicial complex with the filtration value set with \(mini\_ball\_radius(x,y,z))\) iff \(mini\_ball\_radius(x,y,z)) \leq max\_radius\).

And so on for higher dimensions.

Čech complex expansion

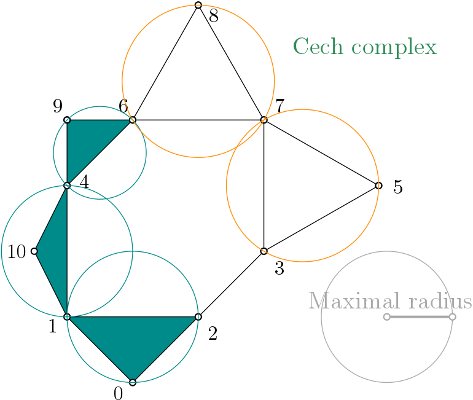
This radius computation is the reason why the Cech_complex is taking much more time to be computed than the Rips complex but it offers more topological guarantees.

If you already have a simplicial complex, it is possible to assign to each simplex a filtration value corresponding to the squared radius of its minimal enclosing ball using assign_MEB_filtration(). This can provide an alternate way of computing a Čech filtration, or it can be used on a Delaunay triangulation to compute a Delaunay-Čech filtration.

Example from a point cloud

This example builds the proximity graph from the given points, and maximal radius values. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Cech_complex.h>
#include <gudhi/Simplex_tree.h>
 
#include <CGAL/Epeck_d.h>  // For EXACT or SAFE version
 
#include <iostream>
#include <string>
#include <vector>
 
int main() {
  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<Gudhi::Simplex_tree_options_fast_persistence>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Kernel = CGAL::Epeck_d<CGAL::Dimension_tag<2>>;
  using Point = typename Kernel::Point_d;
  using Point_cloud = std::vector<Point>;
  using Cech_complex = Gudhi::cech_complex::Cech_complex<Kernel, Simplex_tree>;
 
  Point_cloud points;
  points.emplace_back(1., 0.);                    // 0
  points.emplace_back(0., 1.);                    // 1
  points.emplace_back(2., 1.);                    // 2
  points.emplace_back(3., 2.);                    // 3
  points.emplace_back(0., 3.);                    // 4
  points.emplace_back(3. + std::sqrt(3.), 3.);    // 5
  points.emplace_back(1., 4.);                    // 6
  points.emplace_back(3., 4.);                    // 7
  points.emplace_back(2., 4. + std::sqrt(3.));    // 8
  points.emplace_back(0., 4.);                    // 9
  points.emplace_back(-0.5, 2.);                  // 10
 
  // ----------------------------------------------------------------------------
  // Init of a Cech complex from points
  // ----------------------------------------------------------------------------
  Filtration_value max_radius = 1.;
  Cech_complex cech_complex_from_points(points, max_radius);
 
  Simplex_tree stree;
  cech_complex_from_points.create_complex(stree, 2);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Cech complex
  // ----------------------------------------------------------------------------
  std::clog << "Cech complex is of dimension " << stree.dimension() << " - " << stree.num_simplices() << " simplices - "
            << stree.num_vertices() << " vertices." << std::endl;
 
  std::clog << "Iterator on Cech complex simplices in the filtration order, with [filtration value]:" << std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::clog << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::clog << vertex << " ";
    }
    std::clog << ") -> "
              << "[" << stree.filtration(f_simplex) << "] ";
    std::clog << std::endl;
  }
  return 0;
}

When launching (maximal enclosing ball radius is 1., is expanded until dimension 2):

$> ./Cech_complex_example_from_points

the program output is:

Iterator on Cech complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0]
   ( 1 ) -> [0]
   ( 2 ) -> [0]
   ( 3 ) -> [0]
   ( 4 ) -> [0]
   ( 5 ) -> [0]
   ( 6 ) -> [0]
   ( 7 ) -> [0]
   ( 8 ) -> [0]
   ( 9 ) -> [0]
   ( 10 ) -> [0]
   ( 9 4 ) -> [0.5]
   ( 9 6 ) -> [0.5]
   ( 10 1 ) -> [0.559017]
   ( 10 4 ) -> [0.559017]
   ( 1 0 ) -> [0.707107]
   ( 2 0 ) -> [0.707107]
   ( 3 2 ) -> [0.707107]
   ( 6 4 ) -> [0.707107]
   ( 9 6 4 ) -> [0.707107]
   ( 2 1 ) -> [1]
   ( 2 1 0 ) -> [1]
   ( 4 1 ) -> [1]
   ( 5 3 ) -> [1]
   ( 7 3 ) -> [1]
   ( 7 5 ) -> [1]
   ( 7 6 ) -> [1]
   ( 8 6 ) -> [1]
   ( 8 7 ) -> [1]
   ( 10 4 1 ) -> [1]

Function Documentation

assign_MEB_filtration()

template<bool Output_squared_values = true, typename Kernel , typename SimplicialComplexForMEB , typename PointRange >

void Gudhi::cech_complex::assign_MEB_filtration	(	Kernel &&	k,
		SimplicialComplexForMEB &	complex,
		PointRange const &	points,
		bool	exact = false
	)

Given a simplicial complex and an embedding of its vertices, this assigns to each simplex a filtration value equal to the squared (or not squared in function of Output_squared_values) radius of its minimal enclosing ball (MEB).

Applied on a Čech complex, it recomputes the same values (squared or not in function of Output_squared_values). Applied on a Delaunay triangulation, it computes the Delaunay-Čech filtration.

Template Parameters

Output_squared_values	If true (default value), it assigns to each simplex a filtration value equal to the squared radius of the MEB, or to the radius when Output_squared_values is false.
Kernel	CGAL kernel: either Epick_d or Epeck_d.
PointRange	Random access range of Kernel::Point_d.

Parameters

[in]	k	The geometric kernel.
[in]	complex	The simplicial complex.
[in]	points	Embedding of the vertices of the complex.
[in]	exact	If true and Kernel is CGAL::Epeck_d, the filtration values are computed exactly. Default is false.