Rips complex

Classes
class	Gudhi::rips_complex::Rips_complex< Filtration_value >
	Rips complex data structure. More...
class	Gudhi::rips_complex::Sparse_rips_complex< Filtration_value >
	Sparse Rips complex data structure. More...

Detailed Description

Author

Clément Maria, Pawel Dlotko, Vincent Rouvreau, Marc Glisse

Rips complex definition

The Vietoris-Rips complex (Wikipedia) is an abstract simplicial complex defined on a finite metric space, where each simplex corresponds to a subset of points whose diameter is smaller that some given threshold. Varying the threshold, we can also see the Rips complex as a filtration of the \((n-1)-\)dimensional simplex, where the filtration value of each simplex is the diameter of the corresponding subset of points.

This filtered complex is most often used as an approximation of the Čech complex. After rescaling (Rips using the length of the edges and Čech the half-length), they share the same 1-skeleton and are multiplicatively 2-interleaved or better. While it is slightly bigger, it is also much easier to compute.

The number of simplices in the full Rips complex is exponential in the number of vertices, it is thus usually restricted, by excluding all the simplices with filtration value larger than some threshold, and keeping only the dim_max-skeleton. It may also be a good idea to start by making the point set sparser, for instance with Gudhi::subsampling::sparsify_point_set(), since small clusters of points have a disproportionate cost without affecting the persistence diagram much.

In order to build this complex, the algorithm first builds the graph. The filtration value of each edge is computed from a user-given distance function, or directly read from the distance matrix. In a second step, this graph is inserted in a simplicial complex, which then gets expanded to a flag complex.

The input can be given as a range of points and a distance function, or as a distance matrix.

Vertex name correspond to the index of the point in the given range (aka. the point cloud).

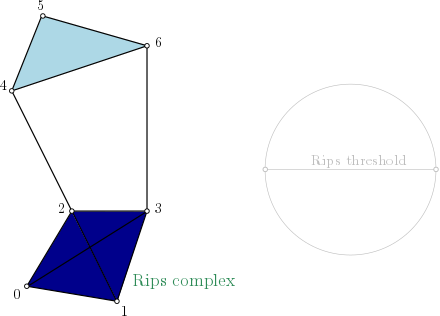
Rips-complex one skeleton graph representation

On this example, as edges (4,5), (4,6) and (5,6) are in the complex, simplex (4,5,6) is added with the filtration value set with \(max(filtration(4,5), filtration(4,6), filtration(5,6))\). And so on for simplex (0,1,2,3).

If the Rips_complex interfaces are not detailed enough for your need, please refer to the example Persistent_cohomology/rips_persistence_step_by_step.cpp , where the constructions of the graph and the Simplex_tree are more detailed.

Sparse Rips complex

Even truncated in filtration value and dimension, the Rips complex remains quite large. However, it is possible to approximate it by a much smaller filtered simplicial complex (linear size, with constants that depend on ε and the doubling dimension of the space) that is \((1+O(\epsilon))-\)interleaved with it (in particular, their persistence diagrams are at log-bottleneck distance at most \(O(\epsilon)\)).

The sparse Rips filtration was introduced by Don Sheehy [45]. We are using the version described in [12] (except that we multiply all filtration values by 2, to match the usual Rips complex), for which [18] proves a \((1,\frac{1}{1-\epsilon})\)-interleaving, although in practice the error is usually smaller. A more intuitive presentation of the idea is available in [18], and in a video [19].

The interface of Sparse_rips_complex is similar to the one for the usual Rips_complex, except that one has to specify the approximation factor. There is an option to limit the minimum and maximum filtration values, but they are not recommended: the way the approximation is done means that larger filtration values are much cheaper to handle than low filtration values, so the gain in ignoring the large ones is small, and Gudhi::subsampling::sparsify_point_set() is a more efficient way of ignoring small filtration values.

Theoretical guarantees are only available for \(\epsilon<1\). The construction accepts larger values of ε, and the size of the complex keeps decreasing, but there is no guarantee on the quality of the result. Note that while the number of edges decreases when ε increases, the number of higher-dimensional simplices may not be monotonous when \(\frac12\leq\epsilon\leq 1\).

Point cloud and distance function

Example from a point cloud and a distance function

This example builds the one skeleton graph from the given points, threshold value, and distance function. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>
 
#include <iostream>
#include <string>
#include <vector>
#include <limits>  // for std::numeric_limits
 
int main() {
  // Type definitions
  using Point = std::vector<double>;
  using Simplex_tree = Gudhi::Simplex_tree<Gudhi::Simplex_tree_options_fast_persistence>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
 
  std::vector<Point> points;
  points.push_back({1.0, 1.0});
  points.push_back({7.0, 0.0});
  points.push_back({4.0, 6.0});
  points.push_back({9.0, 6.0});
  points.push_back({0.0, 14.0});
  points.push_back({2.0, 19.0});
  points.push_back({9.0, 17.0});
 
  // ----------------------------------------------------------------------------
  // Init of a Rips complex from points
  // ----------------------------------------------------------------------------
  double threshold = 12.0;
  Rips_complex rips_complex_from_points(points, threshold, Gudhi::Euclidean_distance());
 
  Simplex_tree stree;
  rips_complex_from_points.create_complex(stree, 1);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Rips complex
  // ----------------------------------------------------------------------------
  std::clog << "Rips complex is of dimension " << stree.dimension() <<
               " - " << stree.num_simplices() << " simplices - " <<
               stree.num_vertices() << " vertices." << std::endl;
 
  std::clog << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
               std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::clog << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::clog << vertex << " ";
    }
    std::clog << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    std::clog << std::endl;
  }
  return 0;
}

When launching (Rips maximal distance between 2 points is 12.0, is expanded until dimension 1 - one skeleton graph in other words):

$> ./Rips_complex_example_one_skeleton_from_points

the program output is:

Rips complex is of dimension 1 - 18 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Example from OFF file

This example builds the Rips_complex from the given points in an OFF file, threshold value, and distance function. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the Rips complex.

#include <gudhi/Rips_complex.h>
// to construct Rips_complex from a OFF file of points
#include <gudhi/Points_off_io.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>
 
#include <iostream>
#include <string>
#include <vector>
 
void usage(int nbArgs, char * const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off threshold dim_max [ouput_file.txt]\n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/alphacomplexdoc.off 60.0\n";
  exit(-1);  // ----- >>
}
 
int main(int argc, char **argv) {
  if ((argc != 4) && (argc != 5)) usage(argc, (argv[0] - 1));
 
  std::string off_file_name(argv[1]);
  double threshold = atof(argv[2]);
  int dim_max = atoi(argv[3]);
 
  // Type definitions
  using Point = std::vector<float>;
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
 
  // ----------------------------------------------------------------------------
  // Init of a Rips complex from an OFF file
  // ----------------------------------------------------------------------------
  Gudhi::Points_off_reader<Point> off_reader(off_file_name);
  Rips_complex rips_complex_from_file(off_reader.get_point_cloud(), threshold, Gudhi::Euclidean_distance());
 
  std::streambuf* streambuffer;
  std::ofstream ouput_file_stream;
 
  if (argc == 5) {
    ouput_file_stream.open(std::string(argv[4]));
    streambuffer = ouput_file_stream.rdbuf();
  } else {
    streambuffer = std::clog.rdbuf();
  }
 
  Simplex_tree stree;
  rips_complex_from_file.create_complex(stree, dim_max);
  std::ostream output_stream(streambuffer);
 
  // ----------------------------------------------------------------------------
  // Display information about the Rips complex
  // ----------------------------------------------------------------------------
  output_stream << "Rips complex is of dimension " << stree.dimension() <<
                   " - " << stree.num_simplices() << " simplices - " <<
                   stree.num_vertices() << " vertices." << std::endl;
 
  output_stream << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
                   std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    output_stream << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      output_stream << vertex << " ";
    }
    output_stream << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    output_stream << std::endl;
  }
 
  ouput_file_stream.close();
  return 0;
}

When launching:

$> ./Rips_complex_example_from_off ../../data/points/alphacomplexdoc.off 12.0 3

the program output is:

Rips complex is of dimension 3 - 24 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 2 1 0 ) -> [6.7082] 
   ( 3 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 3 1 0 ) -> [9.43398] 
   ( 3 2 0 ) -> [9.43398] 
   ( 3 2 1 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 5 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Example of a sparse Rips from a point cloud

This example builds the full sparse Rips of a set of 2D Euclidean points, then prints some minimal information about the complex.

#include <gudhi/Sparse_rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>
 
#include <iostream>
#include <vector>
 
int main() {
  using Point = std::vector<double>;
  using Simplex_tree = Gudhi::Simplex_tree<Gudhi::Simplex_tree_options_fast_persistence>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Sparse_rips = Gudhi::rips_complex::Sparse_rips_complex<Filtration_value>;
 
  Point points[] = {{1.0, 1.0}, {7.0, 0.0}, {4.0, 6.0}, {9.0, 6.0}, {0.0, 14.0}, {2.0, 19.0}, {9.0, 17.0}};
 
  // ----------------------------------------------------------------------------
  // Init from Euclidean points
  // ----------------------------------------------------------------------------
  double epsilon = 2;  // very rough, no guarantees
  Sparse_rips sparse_rips(points, Gudhi::Euclidean_distance(), epsilon);
 
  Simplex_tree stree;
  sparse_rips.create_complex(stree, 10);
 
  // ----------------------------------------------------------------------------
  // Display information about the complex
  // ----------------------------------------------------------------------------
  std::clog << "Sparse Rips complex is of dimension " << stree.dimension() << " - " << stree.num_simplices()
            << " simplices - " << stree.num_vertices() << " vertices." << std::endl;
}

When launching:

$> ./Rips_complex_example_sparse

the program output may be (the exact output varies from one run to the next):

Sparse Rips complex is of dimension 2 - 19 simplices - 7 vertices.

Distance matrix

Example from a distance matrix

This example builds the one skeleton graph from the given distance matrix and threshold value. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>
 
#include <iostream>
#include <string>
#include <vector>
#include <limits>  // for std::numeric_limits
 
int main() {
  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
  using Distance_matrix = std::vector<std::vector<Filtration_value>>;
 
  // User defined distance matrix is:
  // | 0    0.94 0.77 0.99 0.11  |
  // | 0.94 0    0.26 0.99 0.39  |
  // | 0.77 0.26 0    0.28 0.97  |
  // | 0.99 0.99 0.28 0    0.30  |
  // | 0.11 0.39 0.97 0.30 0     |
 
  Distance_matrix distances;
  distances.push_back({});
  distances.push_back({0.94});
  distances.push_back({0.77, 0.26});
  distances.push_back({0.99, 0.99, 0.28});
  distances.push_back({0.11, 0.39, 0.97, 0.30});
 
  // ----------------------------------------------------------------------------
  // Init of a Rips complex from points
  // ----------------------------------------------------------------------------
  double threshold = 1.0;
  Rips_complex rips_complex_from_points(distances, threshold);
 
  Simplex_tree stree;
  rips_complex_from_points.create_complex(stree, 1);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Rips complex
  // ----------------------------------------------------------------------------
  std::clog << "Rips complex is of dimension " << stree.dimension() <<
               " - " << stree.num_simplices() << " simplices - " <<
               stree.num_vertices() << " vertices." << std::endl;
 
  std::clog << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
               std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::clog << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::clog << vertex << " ";
    }
    std::clog << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    std::clog << std::endl;
  }
 
  return 0;
}

When launching (Rips maximal distance between 2 points is 1.0, is expanded until dimension 1 - one skeleton graph with other words):

$> ./Rips_complex_example_one_skeleton_from_distance_matrix

the program output is:

Rips complex is of dimension 1 - 18 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Example from a distance matrix read in a csv file

This example builds the one skeleton graph from the given distance matrix read in a csv file and threshold value. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the Rips complex.

#include <gudhi/Rips_complex.h>
// to construct Rips_complex from a csv file representing a distance matrix
#include <gudhi/reader_utils.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>
 
#include <iostream>
#include <string>
#include <vector>
 
void usage(int nbArgs, char * const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.csv threshold dim_max [ouput_file.txt]\n";
  std::cerr << "       i.e.: " << progName << " ../../data/distance_matrix/full_square_distance_matrix.csv 1.0 3\n";
  exit(-1);  // ----- >>
}
 
int main(int argc, char **argv) {
  if ((argc != 4) && (argc != 5)) usage(argc, (argv[0] - 1));
 
  std::string csv_file_name(argv[1]);
  double threshold = atof(argv[2]);
  int dim_max = atoi(argv[3]);
 
  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
  using Distance_matrix = std::vector<std::vector<Filtration_value>>;
 
  // ----------------------------------------------------------------------------
  // Init of a Rips complex from a distance matrix in a csv file
  // Default separator is ';'
  // ----------------------------------------------------------------------------
  Distance_matrix distances = Gudhi::read_lower_triangular_matrix_from_csv_file<Filtration_value>(csv_file_name);
  Rips_complex rips_complex_from_file(distances, threshold);
 
  std::streambuf* streambuffer;
  std::ofstream ouput_file_stream;
 
  if (argc == 5) {
    ouput_file_stream.open(std::string(argv[4]));
    streambuffer = ouput_file_stream.rdbuf();
  } else {
    streambuffer = std::clog.rdbuf();
  }
 
  Simplex_tree stree;
  rips_complex_from_file.create_complex(stree, dim_max);
  std::ostream output_stream(streambuffer);
 
  // ----------------------------------------------------------------------------
  // Display information about the Rips complex
  // ----------------------------------------------------------------------------
  output_stream << "Rips complex is of dimension " << stree.dimension() <<
                   " - " << stree.num_simplices() << " simplices - " <<
                   stree.num_vertices() << " vertices." << std::endl;
 
  output_stream << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
                   std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    output_stream << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      output_stream << vertex << " ";
    }
    output_stream << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    output_stream << std::endl;
  }
 
  ouput_file_stream.close();
  return 0;
}

When launching:

$> ./Rips_complex_example_from_csv_distance_matrix ../../data/distance_matrix/full_square_distance_matrix.csv 1.0 3

the program output is:

Rips complex is of dimension 3 - 24 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 2 1 0 ) -> [6.7082] 
   ( 3 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 3 1 0 ) -> [9.43398] 
   ( 3 2 0 ) -> [9.43398] 
   ( 3 2 1 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 5 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Correlation matrix

Analogously to the case of distance matrix, Rips complexes can be also constructed based on correlation matrix. Given a correlation matrix M, comportment-wise 1-M is a distance matrix. This example builds the one skeleton graph from the given corelation matrix and threshold value. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>
 
#include <iostream>
#include <string>
#include <vector>
#include <limits>  // for std::numeric_limits
 
int main() {
  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
  using Distance_matrix = std::vector<std::vector<Filtration_value>>;
 
  // User defined correlation matrix is:
  // |1     0.06  0.23  0.01  0.89|
  // |0.06  1     0.74  0.01  0.61|
  // |0.23  0.74  1     0.72  0.03|
  // |0.01  0.01  0.72  1     0.7 |
  // |0.89  0.61  0.03  0.7   1   |
 
  Distance_matrix correlations;
  correlations.push_back({});
  correlations.push_back({0.06});
  correlations.push_back({0.23, 0.74});
  correlations.push_back({0.01, 0.01, 0.72});
  correlations.push_back({0.89, 0.61, 0.03, 0.7});
 
  // ----------------------------------------------------------------------------
  // Convert correlation matrix to a distance matrix:
  // ----------------------------------------------------------------------------
  double threshold = 0;
  for (size_t i = 0; i != correlations.size(); ++i) {
    for (size_t j = 0; j != correlations[i].size(); ++j) {
      // Here we check if our data comes from corelation matrix.
      if ((correlations[i][j] < -1) || (correlations[i][j] > 1)) {
        std::cerr << "The input matrix is not a correlation matrix. The program will now terminate.\n";
        throw "The input matrix is not a correlation matrix. The program will now terminate.\n";
      }
      correlations[i][j] = 1 - correlations[i][j];
      // Here we make sure that we will get the threshold value equal to maximal
      // distance in the matrix.
      if (correlations[i][j] > threshold) threshold = correlations[i][j];
    }
  }
 
  //-----------------------------------------------------------------------------
  // Now the correlation matrix is a distance matrix and can be processed further.
  //-----------------------------------------------------------------------------
  Distance_matrix distances = correlations;
 
  Rips_complex rips_complex_from_points(distances, threshold);
 
  Simplex_tree stree;
  rips_complex_from_points.create_complex(stree, 1);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Rips complex. Note that
  // the filtration displayed here comes from the distance matrix computed
  // above, which is 1 - initial correlation matrix. Only this way, we obtain
  // a complex with filtration. If a correlation matrix is used instead, we would
  // have a reverse filtration (i.e. filtration of boundary of each simplex S
  // is greater or equal to the filtration of S).
  // ----------------------------------------------------------------------------
  std::clog << "Rips complex is of dimension " << stree.dimension() << " - " << stree.num_simplices() << " simplices - "
            << stree.num_vertices() << " vertices." << std::endl;
 
  std::clog << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" << std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::clog << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::clog << vertex << " ";
    }
    std::clog << ") -> "
              << "[" << stree.filtration(f_simplex) << "] ";
    std::clog << std::endl;
  }
 
  return 0;
}

When launching:

$> ./example_one_skeleton_from_correlation_matrix

the program output is:

Rips complex is of dimension 1 - 15 simplices - 5 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 4 0 ) -> [0.11] 
   ( 2 1 ) -> [0.26] 
   ( 3 2 ) -> [0.28] 
   ( 4 3 ) -> [0.3] 
   ( 4 1 ) -> [0.39] 
   ( 2 0 ) -> [0.77] 
   ( 1 0 ) -> [0.94] 
   ( 4 2 ) -> [0.97] 
   ( 3 0 ) -> [0.99] 
   ( 3 1 ) -> [0.99] 

All the other constructions discussed for Rips complex for distance matrix can be also performed for Rips complexes construction from correlation matrices.

Warning

As persistence diagrams points will be under the diagonal, bottleneck distance and persistence graphical tool will not work properly, this is a known issue.