Witness complex user manual¶
|
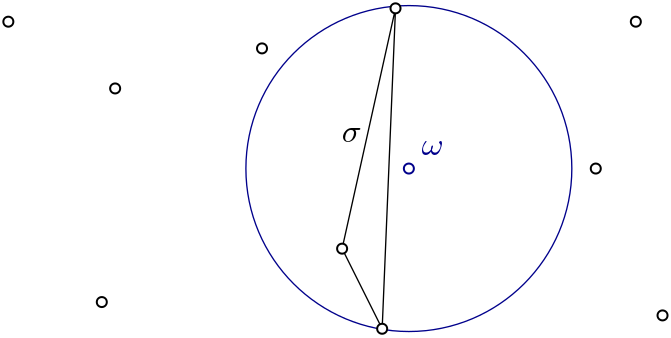
Witness complex \(Wit(W,L)\) is a simplicial complex defined on two sets of points in \(\mathbb{R}^D\). The data structure is described in [5]. |
|
Definitions¶
Witness complex is a simplicial complex defined on two sets of points in \(\mathbb{R}^D\):
\(W\) set of witnesses and
\(L\) set of landmarks.
Even though often the set of landmarks \(L\) is a subset of the set of witnesses \(W\), it is not a requirement for the current implementation.
Landmarks are the vertices of the simplicial complex and witnesses help to decide on which simplices are inserted via a predicate “is witnessed”.
De Silva and Carlsson in their paper [21] differentiate weak witnessing and strong witnessing:
weak: \(\sigma \subset L\) is witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L \setminus \sigma},\ d(w,l) \leq d(w,l')\)
strong: \(\sigma \subset L\) is witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L},\ d(w,l) \leq d(w,l')\)
where \(d(.,.)\) is a distance function.
Both definitions can be relaxed by a real value \(\alpha\):
weak: \(\sigma \subset L\) is \(\alpha\)-witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L \setminus \sigma},\ d(w,l)^2 \leq d(w,l')^2 + \alpha^2\)
strong: \(\sigma \subset L\) is \(\alpha\)-witnessed by \(w \in W\) if \(\forall l \in \sigma,\ \forall l' \in \mathbf{L},\ d(w,l)^2 \leq d(w,l')^2 + \alpha^2\)
which leads to definitions of weak relaxed witness complex (or just relaxed witness complex for short) and strong relaxed witness complex respectively.
Strongly witnessed simplex¶
In particular case of 0-relaxation, weak complex corresponds to witness complex introduced in
[21], whereas 0-relaxed strong witness complex consists of just vertices and is not very
interesting. Hence for small relaxation weak version is preferable.
However, to capture the homotopy type (for example using gudhi.SimplexTree.persistence()) it is
often necessary to work with higher filtration values. In this case strong relaxed witness complex is faster to compute
and offers similar results.
Implementation¶
The two complexes described above are implemented in the corresponding classes
The construction of the Euclidean versions of complexes follow the same scheme:
Construct a search tree on landmarks.
Construct lists of nearest landmarks for each witness.
Construct the witness complex for nearest landmark lists.
In the non-Euclidean classes, the lists of nearest landmarks are supposed to be given as input.
The constructors take on the steps 1 and 2, while the function create_complex() executes the step 3.
Constructing weak relaxed witness complex from an off file¶
Let’s start with a simple example, which reads an off point file and computes a weak witness complex.
import gudhi
import argparse
parser = argparse.ArgumentParser(description='EuclideanWitnessComplex creation from '
'points read in a OFF file.',
epilog='Example: '
'example/witness_complex_diagram_persistence_from_off_file_example.py '
'-f ../data/points/tore3D_300.off -a 1.0 -n 20 -d 2'
'- Constructs a alpha complex with the '
'points from the given OFF file.')
parser.add_argument("-f", "--file", type=str, required=True)
parser.add_argument("-a", "--max_alpha_square", type=float, required=True)
parser.add_argument("-n", "--number_of_landmarks", type=int, required=True)
parser.add_argument("-d", "--limit_dimension", type=int, required=True)
args = parser.parse_args()
with open(args.file, 'r') as f:
first_line = f.readline()
if (first_line == 'OFF\n') or (first_line == 'nOFF\n'):
print("#####################################################################")
print("EuclideanWitnessComplex creation from points read in a OFF file")
witnesses = gudhi.read_points_from_off_file(off_file=args.file)
landmarks = gudhi.pick_n_random_points(points=witnesses, nb_points=args.number_of_landmarks)
message = "EuclideanWitnessComplex with max_edge_length=" + repr(args.max_alpha_square) + \
" - Number of landmarks=" + repr(args.number_of_landmarks)
print(message)
witness_complex = gudhi.EuclideanWitnessComplex(witnesses=witnesses, landmarks=landmarks)
simplex_tree = witness_complex.create_simplex_tree(max_alpha_square=args.max_alpha_square,
limit_dimension=args.limit_dimension)
message = "Number of simplices=" + repr(simplex_tree.num_simplices())
print(message)
else:
print(args.file, "is not a valid OFF file")
f.close()
Example2: Computing persistence using strong relaxed witness complex¶
Here is an example of constructing a strong witness complex filtration and computing persistence on it:
Bibliography¶
- 1
Alon Efrat, Alon Itai, and Matthew J. Katz. Geometry helps in bottleneck matching and related problems. Algorithmica, 31(1):1–28, 2001.
- 2
Michael Kerber, Dmitriy Morozov, and Arnur Nigmetov. Geometry helps to compare persistence diagrams. J. Exp. Algorithmics, 22:1.4:1–1.4:20, September 2017. URL: http://doi.acm.org/10.1145/3064175, doi:10.1145/3064175.
- 3
T. Kaczynski, K. Mischaikow, and M. Mrozek. Computational Homology. Applied Mathematical Sciences. Springer New York, 2004. ISBN 9780387408538. URL: https://books.google.fr/books?id=AShKtpi3GecC.
- 4
Hubert Wagner, Chao Chen, and Erald Vucini. Efficient Computation of Persistent Homology for Cubical Data, pages 91–106. Mathematics and Visualization. Springer Berlin Heidelberg, 2012. URL: http://dx.doi.org/10.1007/978-3-642-23175-9_7, doi:10.1007/978-3-642-23175-9_7.
- 5
Jean-Daniel Boissonnat and Clément Maria. The simplex tree: an efficient data structure for general simplicial complexes. Algorithmica, pages 1–22, 2014. URL: http://dx.doi.org/10.1007/s00453-014-9887-3, doi:10.1007/s00453-014-9887-3.
- 6
Vin de Silva, Dmitriy Morozov, and Mikael Vejdemo-Johansson. Persistent cohomology and circular coordinates. Discrete & Computational Geometry, 45(4):737–759, 2011.
- 7
Tamal K. Dey, Fengtao Fan, and Yusu Wang. Computing topological persistence for simplicial maps. CoRR, 2012.
- 8
Jean-Daniel Boissonnat, Tamal K. Dey, and Clément Maria. The compressed annotation matrix: an efficient data structure for computing persistent cohomology. In ESA, 695–706. 2013. URL: http://dx.doi.org/10.1007/978-3-642-40450-4_59, doi:10.1007/978-3-642-40450-4_59.
- 9
Mathieu Carrière, Bertrand Michel, and Steve Oudot. Statistical Analysis and Parameter Selection for Mapper. CoRR, 2017.
- 10
Tamal Dey, Fengtao Fan, and Yusu Wang. Graph induced complex on point data. In Proceedings of the Twenty-ninth Annual Symposium on Computational Geometry, 107–116. 2013.
- 11
Mathieu Carrière and Steve Oudot. Structure and Stability of the 1-Dimensional Mapper. CoRR, 2015.
- 12
James R. Munkres. Elements of algebraic topology. Addison-Wesley, 1984. ISBN 978-0-201-04586-4.
- 13
Herbert Edelsbrunner and John Harer. Computational Topology - an Introduction. American Mathematical Society, 2010. ISBN 978-0-8218-4925-5.
- 14
Afra Zomorodian and Gunnar E. Carlsson. Computing persistent homology. Discrete & Computational Geometry, 33(2):249–274, 2005.
- 15
Gunnar E. Carlsson and Vin de Silva. Zigzag persistence. Foundations of Computational Mathematics, 10(4):367–405, 2010.
- 16
Donald R. Sheehy. Linear-size approximations to the Vietoris-Rips filtration. Discrete & Computational Geometry, 49(4):778–796, 2013. doi:10.1007/s00454-013-9513-1.
- 17
Mickaël Buchet, Frédéric Chazal, Steve Y. Oudot, and Donald Sheehy. Efficient and robust persistent homology for measures. Computational Geometry: Theory and Applications, 58:70–96, 2016. doi:10.1016/j.comgeo.2016.07.001.
- 18
Nicholas J. Cavanna, Mahmoodreza Jahanseir, and Donald R. Sheehy. A geometric perspective on sparse filtrations. In Proceedings of the Canadian Conference on Computational Geometry. 2015. URL: http://research.cs.queensu.ca/cccg2015/CCCG15-papers/01.pdf.
- 19
Nicholas J. Cavanna, Mahmoodreza Jahanseir, and Donald R. Sheehy. Visualizing sparse filtrations. In Proceedings of the 31st International Symposium on Computational Geometry. 2015. doi:10.4230/LIPIcs.SOCG.2015.23.
- 20
Jean-Daniel Boissonnat and Arijit Ghosh. Manifold reconstruction using tangential delaunay complexes. Discrete & Computational Geometry, 51(1):221–267, 2014. URL: http://dx.doi.org/10.1007/s00454-013-9557-2, doi:10.1007/s00454-013-9557-2.
- 21(1,2)
Vin De Silva and Gunnar Carlsson. Topological estimation using witness complexes. Proc. Sympos. Point-Based Graphics, pages 157–166, 2004.