Čech complex

Classes
class	Gudhi::cech_complex::Cech_complex< Kernel, SimplicialComplexForCechComplex >
	Cech complex class. More...

Detailed Description

Author

Vincent Rouvreau

Čech complex definition

Čech complex (Wikipedia) is a simplicial complex constructed from a proximity graph. The set of all simplices is filtered by the radius of their minimal enclosing ball.

The input shall be a range of points where a point is defined as CGAL kernel Point_d.

Remarks

For people only interested in the topology of the Čech complex (for instance persistence), Alpha complex is equivalent to the Čech complex and much smaller if you do not bound the radii. Čech complex can still make sense in higher dimension precisely because you can bound the radii.

Algorithm

Cech_complex first builds a proximity graph from a point cloud. The filtration value of each edge of the Gudhi::Proximity_graph is computed using CGAL kernel functions.

All edges that have a filtration value strictly greater than a user given maximal radius value, \(max\_radius\), are not inserted into the complex.

Vertex name correspond to the index of the point in the given range (aka. the point cloud).

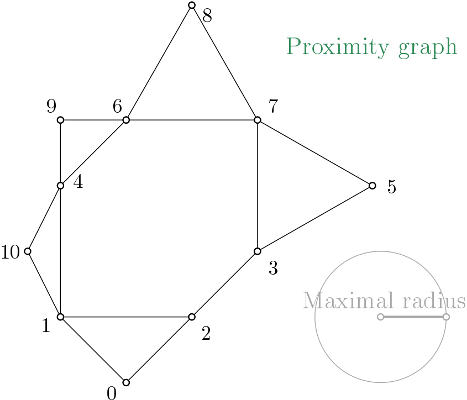
Čech complex proximity graph representation

When creating a simplicial complex from this proximity graph, Cech_complex inserts the proximity graph into the simplicial complex data structure, and then expands the simplicial complex when required.

On this example, as edges \((x,y)\), \((y,z)\) and \((z,y)\) are in the complex, the minimal ball radius containing the points \((x,y,z)\) is computed.

\((x,y,z)\) is inserted to the simplicial complex with the filtration value set with \(mini\_ball\_radius(x,y,z))\) iff \(mini\_ball\_radius(x,y,z)) \leq max\_radius\).

And so on for higher dimensions.

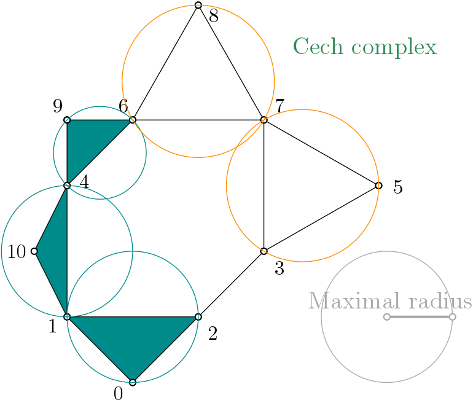
Čech complex expansion

This radius computation is the reason why the Cech_complex is taking much more time to be computed than the Rips complex but it offers more topological guarantees.

Example from a point cloud

This example builds the proximity graph from the given points, and maximal radius values. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Cech_complex.h>
#include <gudhi/Simplex_tree.h>
 
#include <CGAL/Epeck_d.h>  // For EXACT or SAFE version
 
#include <iostream>
#include <string>
#include <vector>
 
int main() {
  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<Gudhi::Simplex_tree_options_fast_persistence>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Kernel = CGAL::Epeck_d<CGAL::Dimension_tag<2>>;
  using Point = typename Kernel::Point_d;
  using Point_cloud = std::vector<Point>;
  using Cech_complex = Gudhi::cech_complex::Cech_complex<Kernel, Simplex_tree>;
 
  Point_cloud points;
  points.emplace_back(1., 0.);                    // 0
  points.emplace_back(0., 1.);                    // 1
  points.emplace_back(2., 1.);                    // 2
  points.emplace_back(3., 2.);                    // 3
  points.emplace_back(0., 3.);                    // 4
  points.emplace_back(3. + std::sqrt(3.), 3.);    // 5
  points.emplace_back(1., 4.);                    // 6
  points.emplace_back(3., 4.);                    // 7
  points.emplace_back(2., 4. + std::sqrt(3.));    // 8
  points.emplace_back(0., 4.);                    // 9
  points.emplace_back(-0.5, 2.);                  // 10
 
  // ----------------------------------------------------------------------------
  // Init of a Cech complex from points
  // ----------------------------------------------------------------------------
  Filtration_value max_radius = 1.;
  Cech_complex cech_complex_from_points(points, max_radius);
 
  Simplex_tree stree;
  cech_complex_from_points.create_complex(stree, 2);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Cech complex
  // ----------------------------------------------------------------------------
  std::clog << "Cech complex is of dimension " << stree.dimension() << " - " << stree.num_simplices() << " simplices - "
            << stree.num_vertices() << " vertices." << std::endl;
 
  std::clog << "Iterator on Cech complex simplices in the filtration order, with [filtration value]:" << std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::clog << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::clog << vertex << " ";
    }
    std::clog << ") -> "
              << "[" << stree.filtration(f_simplex) << "] ";
    std::clog << std::endl;
  }
  return 0;
}

When launching (maximal enclosing ball radius is 1., is expanded until dimension 2):

$> ./Cech_complex_example_from_points

the program output is:

Iterator on Cech complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0]
   ( 1 ) -> [0]
   ( 2 ) -> [0]
   ( 3 ) -> [0]
   ( 4 ) -> [0]
   ( 5 ) -> [0]
   ( 6 ) -> [0]
   ( 7 ) -> [0]
   ( 8 ) -> [0]
   ( 9 ) -> [0]
   ( 10 ) -> [0]
   ( 9 4 ) -> [0.5]
   ( 9 6 ) -> [0.5]
   ( 10 1 ) -> [0.559017]
   ( 10 4 ) -> [0.559017]
   ( 1 0 ) -> [0.707107]
   ( 2 0 ) -> [0.707107]
   ( 3 2 ) -> [0.707107]
   ( 6 4 ) -> [0.707107]
   ( 9 6 4 ) -> [0.707107]
   ( 2 1 ) -> [1]
   ( 2 1 0 ) -> [1]
   ( 4 1 ) -> [1]
   ( 5 3 ) -> [1]
   ( 7 3 ) -> [1]
   ( 7 5 ) -> [1]
   ( 7 6 ) -> [1]
   ( 8 6 ) -> [1]
   ( 8 7 ) -> [1]
   ( 10 4 1 ) -> [1]