Classes | |
| struct | Gudhi::skeleton_blocker::Skeleton_blocker_simple_geometric_traits< GeometryTrait > |
| Simple traits that is a model of SkeletonBlockerGeometricDS and can be passed as a template argument to Skeleton_blocker_geometric_complex. More... | |
| struct | Gudhi::skeleton_blocker::Skeleton_blocker_simple_traits |
| Simple traits that is a model of SkeletonBlockerDS and can be passed as a template argument to Skeleton_blocker_complex. More... | |
| class | Gudhi::skeleton_blocker::Skeleton_blocker_geometric_complex< SkeletonBlockerGeometricDS > |
| Class that represents a geometric complex that can be simplified. The class allows access to points of vertices. More... | |
| class | Gudhi::skeleton_blocker::Skeleton_blocker_link_complex< ComplexType > |
| Class representing the link of a simplicial complex encoded by a skeleton/blockers pair. It inherits from Skeleton_blocker_sub_complex because such complex is a sub complex of a root complex. More... | |
| class | Gudhi::skeleton_blocker::Skeleton_blocker_complex< SkeletonBlockerDS > |
| Abstract Simplicial Complex represented with a skeleton/blockers pair. More... | |
The Skeleton-Blocker data-structure proposes a light encoding for simplicial complexes by storing only an implicit representation of its simplices [2],[3]. Intuitively, it just stores the 1-skeleton of a simplicial complex with a graph and the set of its "missing faces" that is very small in practice (see next section for a formal definition). This data-structure handles all simplicial complexes operations such as as simplex enumeration or simplex removal but operations that are particularly efficient are operations that do not require simplex enumeration such as edge iteration, link computation or simplex contraction.
We recall briefly classical definitions of simplicial complexes
[42]. An abstract simplex is a finite non-empty set and its dimension is its number of elements minus 1. Whenever \(\tau \subset \sigma\) and \(\tau \neq \emptyset \), \( \tau \) is called a face of \( \sigma\) and \( \sigma\) is called a coface of \( \tau \) . Furthermore, when \( \tau \neq \sigma\) we say that \( \tau\) is a proper-face of \( \sigma\). An abstract simplicial complex is a set of simplices that contains all the faces of its simplices. The 1-skeleton of a simplicial complex (or its graph) consists of its elements of dimension lower than 2.
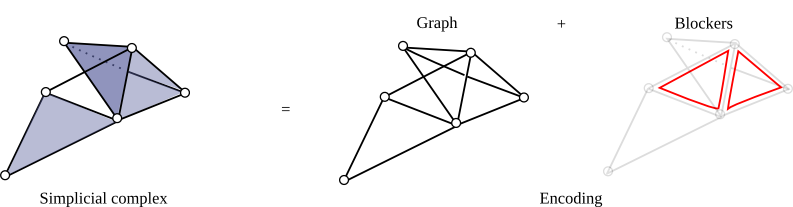
To encode, a simplicial complex, one can encodes all its simplices. In case when this number gets too large, a lighter and implicit version consists of encoding only its graph plus some elements called missing faces or blockers. A blocker is a simplex of dimension greater than 1 that does not belong to the complex but whose all proper faces does.
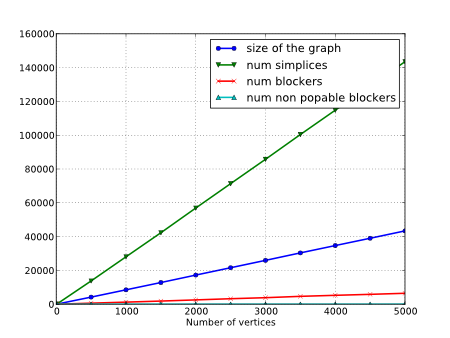
Remark that for a clique complex (i.e. a simplicial complex whose simplices are cliques of its graph), the set of blockers is empty and the data-structure is then particularly sparse. One famous example of clique-complex is the Rips complex which is intensively used in topological data-analysis. In practice, the set of blockers of a simplicial complex remains also small when simplifying a Rips complex with edge contractions but also for most of the simplicial complexes used in topological data-analysis such as Delaunay, Cech or Witness complexes. For instance, the numbers of blockers is depicted for random 3-dimensional spheres embedded into \(R^4\) in next figure. Storing the graph and blockers of such simplicial complexes is much compact in this case than storing their simplices.
Two main classes of this package are Skeleton_blocker_complex and Skeleton_blocker_geometric_complex. The first one can be used to represent an abstract simplicial complex and supports most used operations in a simplicial complex such as :
The class Skeleton_blocker_geometric_complex supports the same methods as Skeleton_blocker_complex and point access in addition.
The class Skeleton_blocker_complex has a visitor that is called when usual operations such as adding an edge or remove a vertex are called. You may want to use this visitor to compute statistics or to update another data-structure (for instance this visitor is heavily used in the Edge contraction package).
Iteration through vertices, edges, simplices or blockers is straightforward with c++11 for range loops. Note that simplex iteration with this implicit data-structure just takes a few more time compared to iteration via an explicit representation such as the Simplex Tree. The following example computes the Euler Characteristic of a simplicial complex.
./SkeletonBlockerIteration Saw 15 vertices, 105 edges and 32767 simplices The Euler Characteristic is 1 0.537302s wall, 0.530000s user + 0.000000s system = 0.530000s CPU (98.6%)
./SkeletonBlockerFromSimplices
Simplices:
{0} {0,1} {0,2} {0,3} {0,1,2} {0,1,3} {0,2,3} {1} {1,2} {1,3} {1,2,3} {2} {2,3} {3}
Blockers: {0,1,2,3}
Simplices:
{0} {0,1} {0,2} {1} {1,2} {2}
Blockers: {0,1,2}
The author wishes to thank Dominique Attali and André Lieutier for their collaboration to write the two initial papers [2],[3] about this data-structure and also Dominique for leaving him use a prototype.