Bottleneck distance

Classes
struct	Gudhi::persistence_diagram::DiagramPoint
	Concept of point in a persistence diagram. std::get<0>(point) must return the birth of the corresponding component and std::get<1>(point) its death. Both should be convertible to double. A valid implementation of this concept is std::pair<double,double>. Death should be larger than birth, death can be std::numeric_limits<double>::infinity() for components which stay alive. More...
struct	Gudhi::persistence_diagram::PersistenceDiagram
	Concept of persistence diagram. It is a range of DiagramPoint. std::begin(diagram) and std::end(diagram) must return corresponding iterators. More...

Functions
template<typename Persistence_diagram1 , typename Persistence_diagram2 >
double	Gudhi::persistence_diagram::bottleneck_distance (const Persistence_diagram1 &diag1, const Persistence_diagram2 &diag2, double e=(std::numeric_limits< double >::min)())
	Function to compute the Bottleneck distance between two persistence diagrams. More...

Detailed Description

Author

François Godi

Definition

The bottleneck distance measures the similarity between two persistence diagrams. It is the shortest distance b for which there exists a perfect matching between the points of the two diagrams (completed with all the points on the diagonal in order to ignore cardinality mismatchs) such that any couple of matched points are at distance at most b, where the distance between points is the sup norm in \(\mathbb{R}^2\) (not the Euclidean distance).

On this picture, the red edges represent the matching. The bottleneck distance is the length of the longest edge.

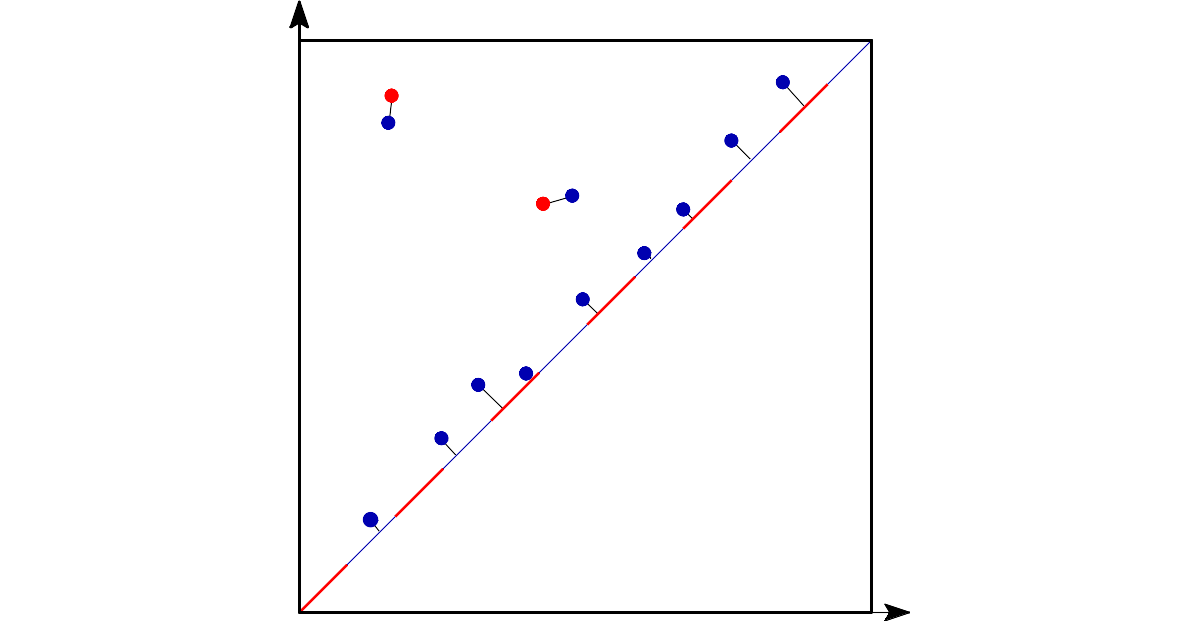
This implementation is based on ideas from "Geometry Helps in Bottleneck Matching and Related Problems" [30]. Another relevant publication, although it was not used is "Geometry Helps to Compare Persistence Diagrams" [38].

Distance computation

The following example explains how the distance is computed:

#include <gudhi/Bottleneck.h>
 
#include <iostream>
#include <vector>
#include <utility>  // for pair
 
int main() {
  std::vector< std::pair<double, double> > diag1, diag2;
  diag1.emplace_back(0., 0.);
  diag2.emplace_back(0., 13.);
 
  double b = Gudhi::persistence_diagram::bottleneck_distance(diag1, diag2);
  std::clog << "Bottleneck distance = " << b << std::endl;
}

Bottleneck distance = 6.5

The point (0, 13) is at distance 6.5 from the diagonal and more specifically from the point (6.5, 6.5)

Basic example

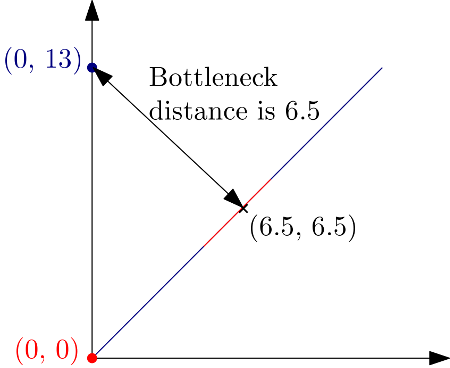
This other example computes the bottleneck distance from 2 persistence diagrams:

#include <gudhi/Bottleneck.h>
 
#include <iostream>
#include <vector>
#include <utility>  // for pair
#include <limits>  // for numeric_limits
 
int main() {
  std::vector< std::pair<double, double> > v1, v2;
 
  v1.emplace_back(2.7, 3.7);
  v1.emplace_back(9.6, 14.);
  v1.emplace_back(34.2, 34.974);
  v1.emplace_back(3., std::numeric_limits<double>::infinity());
 
  v2.emplace_back(2.8, 4.45);
  v2.emplace_back(9.5, 14.1);
  v2.emplace_back(3.2, std::numeric_limits<double>::infinity());
 
 
  double b = Gudhi::persistence_diagram::bottleneck_distance(v1, v2);
 
  std::clog << "Bottleneck distance = " << b << std::endl;
 
  b = Gudhi::persistence_diagram::bottleneck_distance(v1, v2, 0.1);
 
  std::clog << "Approx bottleneck distance = " << b << std::endl;
}

Bottleneck distance = 0.75
Approx bottleneck distance = 0.808176

Function Documentation

bottleneck_distance()

template<typename Persistence_diagram1 , typename Persistence_diagram2 >

double Gudhi::persistence_diagram::bottleneck_distance	(	const Persistence_diagram1 &	diag1,
		const Persistence_diagram2 &	diag2,
		double	e = (std::numeric_limits<double>::min)()
	)

Function to compute the Bottleneck distance between two persistence diagrams.

Template Parameters

Persistence_diagram1,Persistence_diagram2

models of the concept PersistenceDiagram.

Parameters

[in]	diag1	The first persistence diagram.
[in]	diag2	The second persistence diagram.
[in]	e	If e is 0, this uses an expensive algorithm to compute the exact distance. If e is not 0, it asks for an additive e-approximation, and currently also allows a small multiplicative error (the last 2 or 3 bits of the mantissa may be wrong). This version of the algorithm takes advantage of the limited precision of double and is usually a lot faster to compute, whatever the value of e. Thus, by default, e is the smallest positive double.

Examples

alpha_rips_persistence_bottleneck_distance.cpp, bottleneck_basic_example.cpp, and bottleneck_distance.cpp.