Alpha complex

Classes
class	Gudhi::alpha_complex::Alpha_complex< Kernel >
	Alpha complex data structure. More...
class	Gudhi::alpha_complex::Alpha_complex_3d< Complexity, Weighted, Periodic >
	Alpha complex data structure for 3d specific case. More...

Enumerations
enum	Gudhi::alpha_complex::complexity : char { Gudhi::alpha_complex::complexity::FAST = 'f', Gudhi::alpha_complex::complexity::SAFE = 's', Gudhi::alpha_complex::complexity::EXACT = 'e' }
	Alpha complex complexity template parameter possible values. More...

Detailed Description

Author

Vincent Rouvreau

Definition

Alpha_complex is a simplicial complex constructed from the finite cells of a Delaunay Triangulation.

The filtration value of each simplex is computed as the square of the circumradius of the simplex if the circumsphere is empty (the simplex is then said to be Gabriel), and as the minimum of the filtration values of the codimension 1 cofaces that make it not Gabriel otherwise.

All simplices that have a filtration value \( > \alpha^2 \) are removed from the Delaunay complex when creating the simplicial complex if it is specified.

Alpha-complex representation

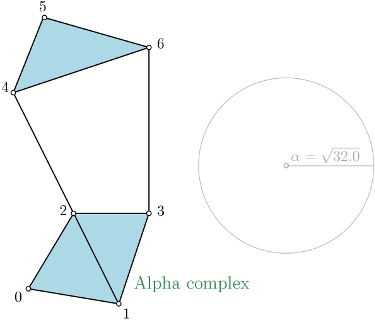
Alpha_complex is constructing a Delaunay Triangulation [24] from CGAL (the Computational Geometry Algorithms Library [41]) and is able to create a SimplicialComplexForAlpha.

The complex is a template class requiring an Epick_d dD Geometry Kernel [39] from CGAL as template parameter.

Remarks

• When the simplicial complex is constructed with an infinite value of \( \alpha^2 \), the complex is a Delaunay complex with special filtration values. The Delaunay complex without filtration values is also available by passing default_filtration_value=true to Alpha_complex::create_complex.
• For people only interested in the topology of the Alpha complex (for instance persistence), Alpha complex is equivalent to the Čech complex and much smaller if you do not bound the radii. Čech complex can still make sense in higher dimension precisely because you can bound the radii.
• Using the default CGAL::Epeck_d makes the construction safe. If you pass exact=true to Alpha_complex::create_complex, the filtration values are the exact ones converted to the filtration value type of the simplicial complex. This can be very slow. If you pass exact=false (the default), the filtration values are only guaranteed to have a small multiplicative error compared to the exact value, see CGAL::Lazy_exact_nt<NT>::set_relative_precision_of_to_double for details. A drawback, when computing persistence, is that an empty exact interval [10^12,10^12] may become a non-empty approximate interval [10^12,10^12+10^6]. Using CGAL::Epick_d makes the computations slightly faster, and the combinatorics are still exact, but the computation of filtration values can exceptionally be arbitrarily bad. In all cases, we still guarantee that the output is a valid filtration (faces have a filtration value no larger than their cofaces).
• For performances reasons, it is advised to use Alpha_complex with CGAL ≥ 5.0.0.

Example from points

This example builds the Delaunay triangulation from the given points in a 2D static kernel, and creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Alpha_complex.h>
// to construct a simplex_tree from alpha complex
#include <gudhi/Simplex_tree.h>

#include <CGAL/Epeck_d.h>

#include <iostream>
#include <vector>

// Explicit dimension 2 Epeck_d kernel
using Kernel = CGAL::Epeck_d< CGAL::Dimension_tag<2> >;
using Point = Kernel::Point_d;
using Vector_of_points = std::vector<Point>;

int main() {
  // ----------------------------------------------------------------------------
  // Init of a list of points
  // ----------------------------------------------------------------------------
  Vector_of_points points;
  points.push_back(Point(1.0, 1.0));
  points.push_back(Point(7.0, 0.0));
  points.push_back(Point(4.0, 6.0));
  points.push_back(Point(9.0, 6.0));
  points.push_back(Point(0.0, 14.0));
  points.push_back(Point(2.0, 19.0));
  points.push_back(Point(9.0, 17.0));

  // ----------------------------------------------------------------------------
  // Init of an alpha complex from the list of points
  // ----------------------------------------------------------------------------
  Gudhi::alpha_complex::Alpha_complex<Kernel> alpha_complex_from_points(points);

  Gudhi::Simplex_tree<> simplex;
  if (alpha_complex_from_points.create_complex(simplex)) {
    // ----------------------------------------------------------------------------
    // Display information about the alpha complex
    // ----------------------------------------------------------------------------
    std::clog << "Alpha complex is of dimension " << simplex.dimension() <<
        " - " << simplex.num_simplices() << " simplices - " <<
        simplex.num_vertices() << " vertices." << std::endl;

    std::clog << "Iterator on alpha complex simplices in the filtration order, with [filtration value]:" << std::endl;
    for (auto f_simplex : simplex.filtration_simplex_range()) {
      std::clog << "   ( ";
      for (auto vertex : simplex.simplex_vertex_range(f_simplex)) {
        std::clog << vertex << " ";
      }
      std::clog << ") -> " << "[" << simplex.filtration(f_simplex) << "] ";
      std::clog << std::endl;
    }
  }
  return 0;
}

When launching:

$> ./Alpha_complex_example_from_points

the program output is:

Alpha complex is of dimension 2 - 25 simplices - 7 vertices.
Iterator on alpha complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [6.25] 
   ( 5 4 ) -> [7.25] 
   ( 2 0 ) -> [8.5] 
   ( 1 0 ) -> [9.25] 
   ( 3 1 ) -> [10] 
   ( 2 1 ) -> [11.25] 
   ( 3 2 1 ) -> [12.5] 
   ( 2 1 0 ) -> [12.9959] 
   ( 6 5 ) -> [13.25] 
   ( 4 2 ) -> [20] 
   ( 6 4 ) -> [22.7367] 
   ( 6 5 4 ) -> [22.7367] 
   ( 6 3 ) -> [30.25] 
   ( 6 2 ) -> [36.5] 
   ( 6 3 2 ) -> [36.5] 
   ( 6 4 2 ) -> [37.2449] 
   ( 4 0 ) -> [59.7107] 
   ( 4 2 0 ) -> [59.7107] 

Create complex algorithm

Data structure

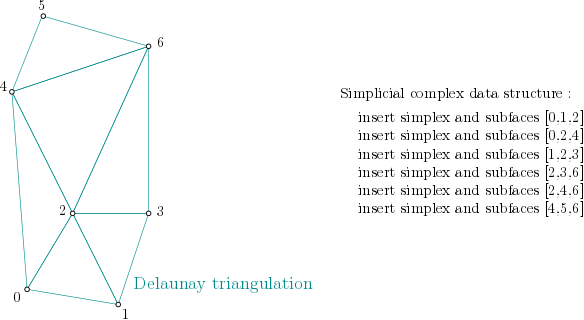
In order to create the simplicial complex, first, it is built from the cells of the Delaunay Triangulation. The filtration values are set to NaN, which stands for unknown value.

In example, :

Simplicial complex structure construction example

Filtration value computation algorithm

\( \textbf{for } \text{i : dimension } \rightarrow 0 \textbf{ do}\\ \quad \textbf{for all } \sigma \text{ of dimension i}\\ \quad\quad \textbf{if } \text{filtration(} \sigma ) \text{ is NaN} \textbf{ then}\\ \quad\quad\quad \text{filtration(} \sigma ) = \alpha^2( \sigma )\\ \quad\quad \textbf{end if}\\ \quad\quad \textbf{for all } \tau \text{ face of } \sigma \textbf{ do}\quad\quad \textit{// propagate alpha filtration value}\\ \quad\quad\quad \textbf{if } \text{filtration(} \tau ) \text{ is not NaN} \textbf{ then}\\ \quad\quad\quad\quad \text{filtration(} \tau \text{) = min( filtration(} \tau \text{), filtration(} \sigma \text{) )}\\ \quad\quad\quad \textbf{else}\\ \quad\quad\quad\quad \textbf{if } \tau \text{ is not Gabriel for } \sigma \textbf{ then}\\ \quad\quad\quad\quad\quad \text{filtration(} \tau \text{) = filtration(} \sigma \text{)}\\ \quad\quad\quad\quad \textbf{end if}\\ \quad\quad\quad \textbf{end if}\\ \quad\quad \textbf{end for}\\ \quad \textbf{end for}\\ \textbf{end for}\\ \text{make_filtration_non_decreasing()}\\ \text{prune_above_filtration()}\\ \)

Dimension 2

From the example above, it means the algorithm looks into each triangle ([0,1,2], [0,2,4], [1,2,3], ...), computes the filtration value of the triangle, and then propagates the filtration value as described here :

Filtration value propagation example

Dimension 1

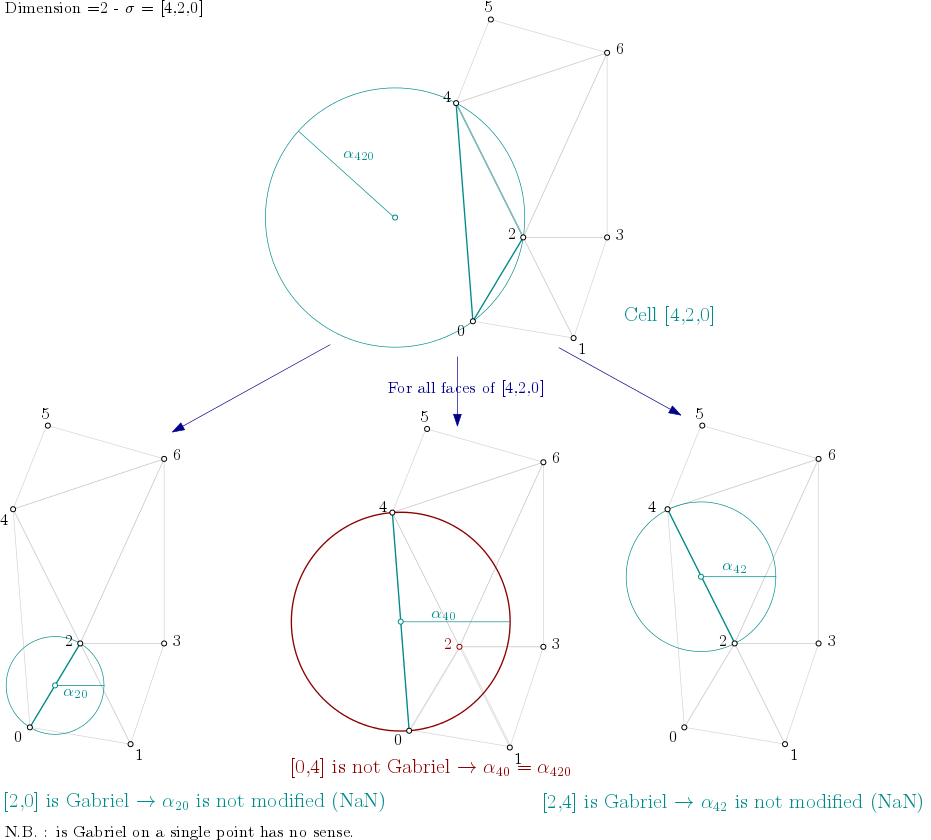
Then, the algorithm looks into each edge ([0,1], [0,2], [1,2], ...), computes the filtration value of the edge (in this case, propagation will have no effect).

Dimension 0

Finally, the algorithm looks into each vertex ([0], [1], [2], [3], [4], [5] and [6]) and sets the filtration value (0 in case of a vertex - propagation will have no effect).

Non decreasing filtration values

As the squared radii computed by CGAL are an approximation, it might happen that these \( \alpha^2 \) values do not quite define a proper filtration (i.e. non-decreasing with respect to inclusion). We fix that up by calling SimplicialComplexForAlpha::make_filtration_non_decreasing().

Prune above given filtration value

The simplex tree is pruned from the given maximum \( \alpha^2 \) value (cf. SimplicialComplexForAlpha::prune_above_filtration()). In the following example, the value is given by the user as argument of the program.

Example from OFF file

This example builds the Delaunay triangulation in a dynamic kernel, and initializes the alpha complex with it.

Then, it is asked to display information about the alpha complex.

#include <gudhi/Alpha_complex.h>
// to construct a simplex_tree from alpha complex
#include <gudhi/Simplex_tree.h>

#include <iostream>
#include <string>

void usage(int nbArgs, char * const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off alpha_square_max_value [ouput_file.txt]\n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/alphacomplexdoc.off 60.0\n";
  exit(-1);  // ----- >>
}

int main(int argc, char **argv) {
  if ((argc != 3) && (argc != 4)) usage(argc, (argv[0] - 1));

  std::string off_file_name {argv[1]};
  double alpha_square_max_value {atof(argv[2])};

  // ----------------------------------------------------------------------------
  // Init of an alpha complex from an OFF file
  // ----------------------------------------------------------------------------
  Gudhi::alpha_complex::Alpha_complex<> alpha_complex_from_file(off_file_name);

  std::streambuf* streambuffer;
  std::ofstream ouput_file_stream;

  if (argc == 4) {
    ouput_file_stream.open(std::string(argv[3]));
    streambuffer = ouput_file_stream.rdbuf();
  } else {
    streambuffer = std::clog.rdbuf();
  }

  Gudhi::Simplex_tree<> simplex;
  if (alpha_complex_from_file.create_complex(simplex, alpha_square_max_value)) {
    std::ostream output_stream(streambuffer);

    // ----------------------------------------------------------------------------
    // Display information about the alpha complex
    // ----------------------------------------------------------------------------
    output_stream << "Alpha complex is of dimension " << simplex.dimension() <<
        " - " << simplex.num_simplices() << " simplices - " <<
        simplex.num_vertices() << " vertices." << std::endl;

    output_stream << "Iterator on alpha complex simplices in the filtration order, with [filtration value]:" <<
        std::endl;
    for (auto f_simplex : simplex.filtration_simplex_range()) {
      output_stream << "   ( ";
      for (auto vertex : simplex.simplex_vertex_range(f_simplex)) {
        output_stream << vertex << " ";
      }
      output_stream << ") -> " << "[" << simplex.filtration(f_simplex) << "] ";
      output_stream << std::endl;
    }
  }
  ouput_file_stream.close();
  return 0;
}

When launching:

$> ./Alpha_complex_example_from_off ../../data/points/alphacomplexdoc.off 32.0

the program output is:

Alpha complex is of dimension 2 - 20 simplices - 7 vertices.
Iterator on alpha complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [6.25] 
   ( 5 4 ) -> [7.25] 
   ( 2 0 ) -> [8.5] 
   ( 1 0 ) -> [9.25] 
   ( 3 1 ) -> [10] 
   ( 2 1 ) -> [11.25] 
   ( 3 2 1 ) -> [12.5] 
   ( 2 1 0 ) -> [12.9959] 
   ( 6 5 ) -> [13.25] 
   ( 4 2 ) -> [20] 
   ( 6 4 ) -> [22.7367] 
   ( 6 5 4 ) -> [22.7367] 
   ( 6 3 ) -> [30.25] 

3d specific example

A specific module for Alpha complex is available in 3d (cf. Alpha_complex_3d) and allows to construct standard, weighted, periodic or weighted and periodic versions of alpha complexes. Alpha values computation can be Gudhi::alpha_complex::complexity::FAST, Gudhi::alpha_complex::complexity::SAFE (default value) or Gudhi::alpha_complex::complexity::EXACT.

This example builds the CGAL 3d weighted alpha shapes from a small molecule, and initializes the alpha complex with it. This example is taken from CGAL 3d weighted alpha shapes.

Then, it is asked to display information about the alpha complex.

#include <gudhi/Alpha_complex_3d.h>
// to construct a simplex_tree from alpha complex
#include <gudhi/Simplex_tree.h>

#include <iostream>
#include <string>
#include <vector>
#include <limits>  // for numeric limits

// Complexity = FAST, weighted = true, periodic = false
using Weighted_alpha_complex_3d =
    Gudhi::alpha_complex::Alpha_complex_3d<Gudhi::alpha_complex::complexity::SAFE, true, false>;
using Bare_point = Weighted_alpha_complex_3d::Bare_point_3;
using Weighted_point = Weighted_alpha_complex_3d::Weighted_point_3;

int main(int argc, char **argv) {
  // ----------------------------------------------------------------------------
  // Init of a list of points and weights from a small molecule
  // ----------------------------------------------------------------------------
  std::vector<Weighted_point> weighted_points;
  weighted_points.push_back(Weighted_point(Bare_point(1, -1, -1), 4.));
  weighted_points.push_back(Weighted_point(Bare_point(-1, 1, -1), 4.));
  weighted_points.push_back(Weighted_point(Bare_point(-1, -1, 1), 4.));
  weighted_points.push_back(Weighted_point(Bare_point(1, 1, 1), 4.));
  weighted_points.push_back(Weighted_point(Bare_point(2, 2, 2), 1.));

  // ----------------------------------------------------------------------------
  // Init of an alpha complex from the list of points
  // ----------------------------------------------------------------------------
  Weighted_alpha_complex_3d alpha_complex_from_points(weighted_points);

  Gudhi::Simplex_tree<> simplex;
  if (alpha_complex_from_points.create_complex(simplex)) {
    // ----------------------------------------------------------------------------
    // Display information about the alpha complex
    // ----------------------------------------------------------------------------
    std::clog << "Alpha complex is of dimension " << simplex.dimension() << " - " << simplex.num_simplices()
              << " simplices - " << simplex.num_vertices() << " vertices." << std::endl;

    std::clog << "Iterator on alpha complex simplices in the filtration order, with [filtration value]:" << std::endl;
    for (auto f_simplex : simplex.filtration_simplex_range()) {
      std::clog << "   ( ";
      for (auto vertex : simplex.simplex_vertex_range(f_simplex)) {
        std::clog << vertex << " ";
      }
      std::clog << ") -> "
                << "[" << simplex.filtration(f_simplex) << "] ";
      std::clog << std::endl;
    }
  }
  return 0;
}

When launching:

$> ./Alpha_complex_example_weighted_3d_from_points

the program output is:

Alpha complex is of dimension 3 - 29 simplices - 5 vertices.
Iterator on alpha complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [-4] 
   ( 1 ) -> [-4] 
   ( 2 ) -> [-4] 
   ( 3 ) -> [-4] 
   ( 1 0 ) -> [-2] 
   ( 2 0 ) -> [-2] 
   ( 2 1 ) -> [-2] 
   ( 3 0 ) -> [-2] 
   ( 3 1 ) -> [-2] 
   ( 3 2 ) -> [-2] 
   ( 2 1 0 ) -> [-1.33333] 
   ( 3 1 0 ) -> [-1.33333] 
   ( 3 2 0 ) -> [-1.33333] 
   ( 3 2 1 ) -> [-1.33333] 
   ( 3 2 1 0 ) -> [-1] 
   ( 4 ) -> [-1] 
   ( 4 2 ) -> [-1] 
   ( 4 0 ) -> [23] 
   ( 4 1 ) -> [23] 
   ( 4 2 0 ) -> [23] 
   ( 4 2 1 ) -> [23] 
   ( 4 3 ) -> [23] 
   ( 4 3 2 ) -> [23] 
   ( 4 1 0 ) -> [95] 
   ( 4 2 1 0 ) -> [95] 
   ( 4 3 0 ) -> [95] 
   ( 4 3 1 ) -> [95] 
   ( 4 3 2 0 ) -> [95] 
   ( 4 3 2 1 ) -> [95] 

Enumeration Type Documentation

complexity

enum Gudhi::alpha_complex::complexity : char

strong

Alpha complex complexity template parameter possible values.

Enumerator
FAST	Fast version.
SAFE	Safe version.
EXACT	Exact version.

Examples:

Alpha_complex/alpha_complex_3d_persistence.cpp.