A simplicial complex \(\mathbf{K}\) on a set of vertices \(V = \{1, \cdots ,|V|\}\) is a collection of simplices \(\{\sigma\}\), \(\sigma \subseteq V\) such that \(\tau \subseteq \sigma \in \mathbf{K} \rightarrow \tau \in \mathbf{K}\). The dimension \(n=|\sigma|-1\) of \(\sigma\) is its number of elements minus \(1\).
A filtration of a simplicial complex is a function \(f:\mathbf{K} \rightarrow \mathbb{R}\) satisfying \(f(\tau)\leq f(\sigma)\) whenever \(\tau \subseteq \sigma\). Ordering the simplices by increasing filtration values (breaking ties so as a simplex appears after its subsimplices of same filtration value) provides an indexing scheme.
There are two implementation of complexes. The first on is the Simplex_tree data structure. The simplex tree is an efficient and flexible data structure for representing general (filtered) simplicial complexes. The data structure is described in [7]
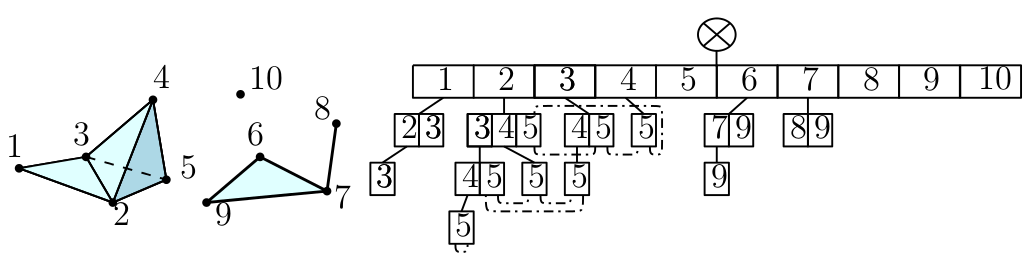
Here is a list of simplex tree examples :
Simplex tree construction with \(\mathbb{Z}/3\mathbb{Z}\) coefficients on weighted graph Klein bottle file:
The second one is the Hasse_complex. The Hasse complex is a data structure representing explicitly all co-dimension 1 incidence relations in a complex. It is consequently faster when accessing the boundary of a simplex, but is less compact and harder to construct from scratch.
| GUDHI Version 3.1.1 - C++ library for Topological Data Analysis (TDA) and Higher Dimensional Geometry Understanding. - Copyright : MIT | Generated on Fri Feb 7 2020 16:35:36 for GUDHI by Doxygen 1.8.13 |