Bottleneck distance

Classes
struct	Gudhi::persistence_diagram::DiagramPoint
	Concept of point in a persistence diagram. std::get<0>(point) must return the birth of the corresponding component and std::get<1>(point) its death. Both should be convertible to double. A valid implementation of this concept is std::pair<double,double>. Death should be larger than birth, death can be std::numeric_limits<double>::infinity() for components which stay alive. More...
struct	Gudhi::persistence_diagram::PersistenceDiagram
	Concept of persistence diagram. It is a range of DiagramPoint. std::begin(diagram) and std::end(diagram) must return corresponding iterators. More...

Functions
template<typename Persistence_diagram1 , typename Persistence_diagram2 >
double	Gudhi::persistence_diagram::bottleneck_distance (const Persistence_diagram1 &diag1, const Persistence_diagram2 &diag2, double e=(std::numeric_limits< double >::min)())
	Function to compute the Bottleneck distance between two persistence diagrams. More...

Detailed Description

Author

François Godi

Definition

The bottleneck distance measures the similarity between two persistence diagrams. It is the shortest distance b for which there exists a perfect matching between the points of the two diagrams (completed with all the points on the diagonal in order to ignore cardinality mismatchs) such that any couple of matched points are at distance at most b.

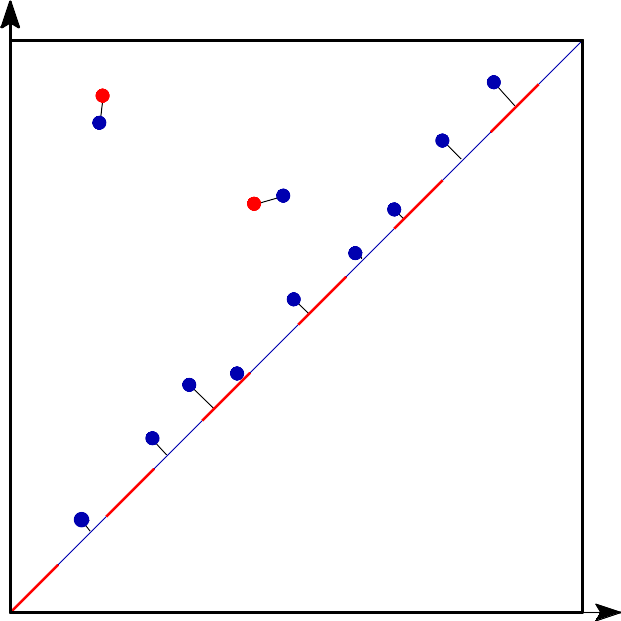
On this picture, the red edges represent the matching. The bottleneck distance is the length of the longest edge.

Function Documentation

bottleneck_distance()

template<typename Persistence_diagram1 , typename Persistence_diagram2 >

double Gudhi::persistence_diagram::bottleneck_distance	(	const Persistence_diagram1 &	diag1,
		const Persistence_diagram2 &	diag2,
		double	e = (std::numeric_limits<double>::min)()
	)

Function to compute the Bottleneck distance between two persistence diagrams.

Template Parameters

Persistence_diagram1,Persistence_diagram2

models of the concept PersistenceDiagram.

Parameters

[in]

e

If e is 0, this uses an expensive algorithm to compute the exact distance. If e is not 0, it asks for an additive e-approximation, and currently also allows a small multiplicative error (the last 2 or 3 bits of the mantissa may be wrong). This version of the algorithm takes advantage of the limited precision of double and is usually a lot faster to compute, whatever the value of e. Thus, by default, e is the smallest positive double.

Examples:

Bottleneck_distance/alpha_rips_persistence_bottleneck_distance.cpp, Bottleneck_distance/bottleneck_basic_example.cpp, and Bottleneck_distance/bottleneck_distance.cpp.