Filtered Complexes

Classes
class	Gudhi::Simplex_tree< SimplexTreeOptions >
	Simplex Tree data structure for representing simplicial complexes. More...
class	Gudhi::Simplex_tree_simplex_vertex_iterator< SimplexTree >
	Iterator over the vertices of a simplex in a SimplexTree. More...
class	Gudhi::Simplex_tree_boundary_simplex_iterator< SimplexTree >
	Iterator over the simplices of the boundary of a simplex. More...
class	Gudhi::Simplex_tree_boundary_opposite_vertex_simplex_iterator< SimplexTree >
	Iterator over the simplices of the boundary of a simplex and their opposite vertices. More...
class	Gudhi::Simplex_tree_complex_simplex_iterator< SimplexTree >
	Iterator over the simplices of a simplicial complex. More...
class	Gudhi::Simplex_tree_skeleton_simplex_iterator< SimplexTree >
	Iterator over the simplices of the skeleton of a given dimension of the simplicial complex. More...
struct	Gudhi::Simplex_tree_node_explicit_storage< SimplexTree >
	Node of a simplex tree with filtration value and simplex key. More...
struct	Gudhi::Simplex_tree_options_default
struct	Gudhi::Simplex_tree_options_full_featured
struct	Gudhi::Simplex_tree_options_minimal
class	Gudhi::Simplex_tree_siblings< SimplexTree, MapContainer >
	Data structure to store a set of nodes in a SimplexTree sharing the same parent node. More...
class	Extended_simplex_type
	Extended simplex type data structure for representing the type of simplices in an extended filtration. More...

Detailed Description

Author

Clément Maria

A simplicial complex \(\mathbf{K}\) on a set of vertices \(V = \{1, \cdots ,|V|\}\) is a collection of simplices \(\{\sigma\}\), \(\sigma \subseteq V\) such that \(\tau \subseteq \sigma \in \mathbf{K} \rightarrow \tau \in \mathbf{K}\). The dimension \(n=|\sigma|-1\) of \(\sigma\) is its number of elements minus \(1\).

A filtration of a simplicial complex is a function \(f:\mathbf{K} \rightarrow \mathbb{R}\) satisfying \(f(\tau)\leq f(\sigma)\) whenever \(\tau \subseteq \sigma\). Ordering the simplices by increasing filtration values (breaking ties so as a simplex appears after its subsimplices of same filtration value) provides an indexing scheme.

Implementations

Simplex tree

There are two implementation of complexes. The first on is the Simplex_tree data structure. The simplex tree is an efficient and flexible data structure for representing general (filtered) simplicial complexes. The data structure is described in [7]

Simplex tree representation

Examples

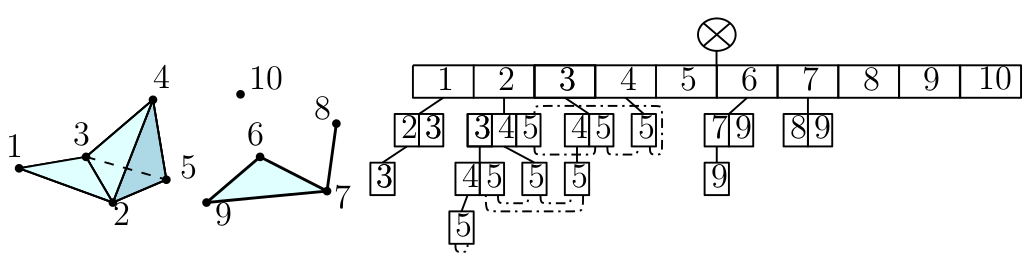
Here is a list of simplex tree examples :

• Simplex_tree/simple_simplex_tree.cpp - Simple simplex tree construction and basic function use.

• Simplex_tree/simplex_tree_from_cliques_of_graph.cpp - Simplex tree construction from cliques of graph read in a file.

Simplex tree construction with \(\mathbb{Z}/3\mathbb{Z}\) coefficients on weighted graph Klein bottle file:

$> ./simplex_tree_from_cliques_of_graph ../../data/points/Klein_bottle_complex.txt 3 

 Insert the 1-skeleton in the simplex tree in 0.000404 s. 
max_dim = 3
Expand the simplex tree in 3.8e-05 s. 
Information of the Simplex Tree: 
Number of vertices = 10   Number of simplices = 98 

• Simplex_tree/example_alpha_shapes_3_simplex_tree_from_off_file.cpp - Simplex tree is computed and displayed from a 3D alpha complex (Requires CGAL, GMP and GMPXX to be installed).

• Simplex_tree/graph_expansion_with_blocker.cpp - Simple simplex tree construction from a one-skeleton graph with a simple blocker expansion method.

Hasse complex

The second one is the Hasse_complex. The Hasse complex is a data structure representing explicitly all co-dimension 1 incidence relations in a complex. It is consequently faster when accessing the boundary of a simplex, but is less compact and harder to construct from scratch.

Iterators and range types for the Simplex_tree.

Represents a node of a Simplex_tree.

Pre-defined options for the Simplex_tree.

Represents a set of node of a Simplex_tree that share the same parent.