Filtered Complexes

Detailed Description

Author

Clément Maria

A simplicial complex $\mathbf{K}$ on a set of vertices $V = \{1, \cdots ,|V|\}$ is a collection of simplices $\{\sigma\}$, $\sigma \subseteq V$ such that $\tau \subseteq \sigma \in \mathbf{K} \rightarrow \tau \in \mathbf{K}$. The dimension $n=|\sigma|-1$ of $\sigma$ is its number of elements minus $1$.

A filtration of a simplicial complex is a function $f:\mathbf{K} \rightarrow \mathbb{R}$ satisfying $f(\tau)\leq f(\sigma)$ whenever $\tau \subseteq \sigma$. Ordering the simplices by increasing filtration values (breaking ties so as a simplex appears after its subsimplices of same filtration value) provides an indexing scheme.

Implementations

Simplex tree

There are two implementation of complexes. The first on is the Simplex_tree data structure. The simplex tree is an efficient and flexible data structure for representing general (filtered) simplicial complexes. The data structure is described in [7]

Simplex tree representation

Examples

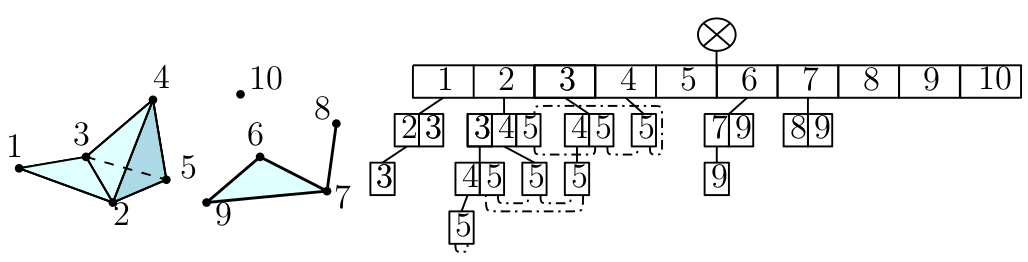
Here is a list of simplex tree examples :

• Simplex_tree/simple_simplex_tree.cpp - Simple simplex tree construction and basic function use.

• Simplex_tree/simplex_tree_from_cliques_of_graph.cpp - Simplex tree construction from cliques of graph read in a file.

Simplex tree construction with $\mathbb{Z}/3\mathbb{Z}$ coefficients on weighted graph Klein bottle file:

$> ./simplex_tree_from_cliques_of_graph ../../data/points/Klein_bottle_complex.txt 3 

 Insert the 1-skeleton in the simplex tree in 0.000404 s. 
max_dim = 3
Expand the simplex tree in 3.8e-05 s. 
Information of the Simplex Tree: 
Number of vertices = 10   Number of simplices = 98 

• Simplex_tree/example_alpha_shapes_3_simplex_tree_from_off_file.cpp - Simplex tree is computed and displayed from a 3D alpha complex (Requires CGAL, GMP and GMPXX to be installed).

• Simplex_tree/graph_expansion_with_blocker.cpp - Simple simplex tree construction from a one-skeleton graph with a simple blocker expansion method.

Hasse complex

The second one is the Hasse_complex. The Hasse complex is a data structure representing explicitly all co-dimension 1 incidence relations in a complex. It is consequently faster when accessing the boundary of a simplex, but is less compact and harder to construct from scratch.