Rips complex

Classes
class	Gudhi::rips_complex::Rips_complex< Filtration_value >
	Rips complex data structure. More...

Detailed Description

Author

Clément Maria, Pawel Dlotko, Vincent Rouvreau

Rips complex definition

Rips_complex (Wikipedia) is a one skeleton graph that allows to construct a simplicial complex from it. The input can be a point cloud with a given distance function, or a distance matrix.

The filtration value of each edge is computed from a user-given distance function, or directly from the distance matrix.

All edges that have a filtration value strictly greater than a given threshold value are not inserted into the complex.

When creating a simplicial complex from this one skeleton graph, Rips inserts the one skeleton graph into the data structure, and then expands the simplicial complex when required.

Vertex name correspond to the index of the point in the given range (aka. the point cloud).

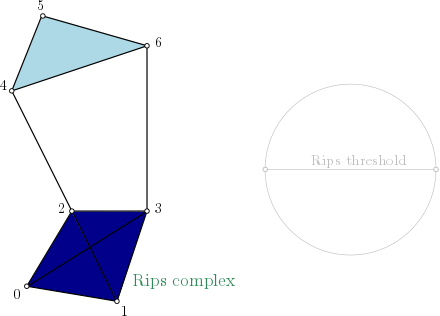
Rips-complex one skeleton graph representation

On this example, as edges (4,5), (4,6) and (5,6) are in the complex, simplex (4,5,6) is added with the filtration value set with \(max(filtration(4,5), filtration(4,6), filtration(5,6))\). And so on for simplex (0,1,2,3).

If the Rips_complex interfaces are not detailed enough for your need, please refer to rips_persistence_step_by_step.cpp example, where the graph construction over the Simplex_tree is more detailed.

Point cloud and distance function

Example from a point cloud and a distance function

This example builds the one skeleton graph from the given points, threshold value, and distance function. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>

#include <iostream>
#include <string>
#include <vector>
#include <limits>  // for std::numeric_limits

int main() {
  // Type definitions
  using Point = std::vector<double>;
  using Simplex_tree = Gudhi::Simplex_tree<Gudhi::Simplex_tree_options_fast_persistence>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;

  std::vector<Point> points;
  points.push_back({1.0, 1.0});
  points.push_back({7.0, 0.0});
  points.push_back({4.0, 6.0});
  points.push_back({9.0, 6.0});
  points.push_back({0.0, 14.0});
  points.push_back({2.0, 19.0});
  points.push_back({9.0, 17.0});

  // ----------------------------------------------------------------------------
  // Init of a Rips complex from points
  // ----------------------------------------------------------------------------
  double threshold = 12.0;
  Rips_complex rips_complex_from_points(points, threshold, Gudhi::Euclidean_distance());

  Simplex_tree stree;
  rips_complex_from_points.create_complex(stree, 1);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Rips complex
  // ----------------------------------------------------------------------------
  std::cout << "Rips complex is of dimension " << stree.dimension() <<
               " - " << stree.num_simplices() << " simplices - " <<
               stree.num_vertices() << " vertices." << std::endl;

  std::cout << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
               std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::cout << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::cout << vertex << " ";
    }
    std::cout << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    std::cout << std::endl;
  }
  return 0;
}

When launching (Rips maximal distance between 2 points is 12.0, is expanded until dimension 1 - one skeleton graph in other words):

$> ./Rips_complex_example_one_skeleton_from_points

the program output is:

Rips complex is of dimension 1 - 18 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Example from OFF file

This example builds the Rips_complex from the given points in an OFF file, threshold value, and distance function. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the Rips complex.

#include <gudhi/Rips_complex.h>
// to construct Rips_complex from a OFF file of points
#include <gudhi/Points_off_io.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>

#include <iostream>
#include <string>
#include <vector>

void usage(int nbArgs, char * const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.off threshold dim_max [ouput_file.txt]\n";
  std::cerr << "       i.e.: " << progName << " ../../data/points/alphacomplexdoc.off 60.0\n";
  exit(-1);  // ----- >>
}

int main(int argc, char **argv) {
  if ((argc != 4) && (argc != 5)) usage(argc, (argv[0] - 1));

  std::string off_file_name(argv[1]);
  double threshold = atof(argv[2]);
  int dim_max = atoi(argv[3]);

  // Type definitions
  using Point = std::vector<float>;
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;

  // ----------------------------------------------------------------------------
  // Init of a Rips complex from an OFF file
  // ----------------------------------------------------------------------------
  Gudhi::Points_off_reader<Point> off_reader(off_file_name);
  Rips_complex rips_complex_from_file(off_reader.get_point_cloud(), threshold, Gudhi::Euclidean_distance());

  std::streambuf* streambufffer;
  std::ofstream ouput_file_stream;

  if (argc == 5) {
    ouput_file_stream.open(std::string(argv[4]));
    streambufffer = ouput_file_stream.rdbuf();
  } else {
    streambufffer = std::cout.rdbuf();
  }

  Simplex_tree stree;
  rips_complex_from_file.create_complex(stree, dim_max);
  std::ostream output_stream(streambufffer);

  // ----------------------------------------------------------------------------
  // Display information about the Rips complex
  // ----------------------------------------------------------------------------
  output_stream << "Rips complex is of dimension " << stree.dimension() <<
                   " - " << stree.num_simplices() << " simplices - " <<
                   stree.num_vertices() << " vertices." << std::endl;

  output_stream << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
                   std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    output_stream << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      output_stream << vertex << " ";
    }
    output_stream << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    output_stream << std::endl;
  }

  ouput_file_stream.close();
  return 0;
}

When launching:

$> ./Rips_complex_example_from_off ../../data/points/alphacomplexdoc.off 12.0 3

the program output is:

Rips complex is of dimension 3 - 24 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 2 1 0 ) -> [6.7082] 
   ( 3 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 3 1 0 ) -> [9.43398] 
   ( 3 2 0 ) -> [9.43398] 
   ( 3 2 1 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 5 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Distance matrix

Example from a distance matrix

This example builds the one skeleton graph from the given distance matrix and threshold value. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the simplicial complex.

#include <gudhi/Rips_complex.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>

#include <iostream>
#include <string>
#include <vector>
#include <limits>  // for std::numeric_limits

int main() {
  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
  using Distance_matrix = std::vector<std::vector<Filtration_value>>;

  // User defined distance matrix is:
  // | 0    0.94 0.77 0.99 0.11  |
  // | 0.94 0    0.26 0.99 0.39  |
  // | 0.77 0.26 0    0.28 0.97  |
  // | 0.99 0.99 0.28 0    0.30  |
  // | 0.11 0.39 0.97 0.30 0     |

  Distance_matrix distances;
  distances.push_back({});
  distances.push_back({0.94});
  distances.push_back({0.77, 0.26});
  distances.push_back({0.99, 0.99, 0.28});
  distances.push_back({0.11, 0.39, 0.97, 0.30});

  // ----------------------------------------------------------------------------
  // Init of a Rips complex from points
  // ----------------------------------------------------------------------------
  double threshold = 1.0;
  Rips_complex rips_complex_from_points(distances, threshold);

  Simplex_tree stree;
  rips_complex_from_points.create_complex(stree, 1);
  // ----------------------------------------------------------------------------
  // Display information about the one skeleton Rips complex
  // ----------------------------------------------------------------------------
  std::cout << "Rips complex is of dimension " << stree.dimension() <<
               " - " << stree.num_simplices() << " simplices - " <<
               stree.num_vertices() << " vertices." << std::endl;

  std::cout << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
               std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    std::cout << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      std::cout << vertex << " ";
    }
    std::cout << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    std::cout << std::endl;
  }

  return 0;
}

When launching (Rips maximal distance between 2 points is 1.0, is expanded until dimension 1 - one skeleton graph with other words):

$> ./Rips_complex_example_one_skeleton_from_distance_matrix

the program output is:

Rips complex is of dimension 1 - 18 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Example from a distance matrix read in a csv file

This example builds the one skeleton graph from the given distance matrix read in a csv file and threshold value. Then it creates a Simplex_tree with it.

Then, it is asked to display information about the Rips complex.

#include <gudhi/Rips_complex.h>
// to construct Rips_complex from a csv file representing a distance matrix
#include <gudhi/reader_utils.h>
#include <gudhi/Simplex_tree.h>
#include <gudhi/distance_functions.h>

#include <iostream>
#include <string>
#include <vector>

void usage(int nbArgs, char * const progName) {
  std::cerr << "Error: Number of arguments (" << nbArgs << ") is not correct\n";
  std::cerr << "Usage: " << progName << " filename.csv threshold dim_max [ouput_file.txt]\n";
  std::cerr << "       i.e.: " << progName << " ../../data/distance_matrix/full_square_distance_matrix.csv 1.0 3\n";
  exit(-1);  // ----- >>
}

int main(int argc, char **argv) {
  if ((argc != 4) && (argc != 5)) usage(argc, (argv[0] - 1));

  std::string csv_file_name(argv[1]);
  double threshold = atof(argv[2]);
  int dim_max = atoi(argv[3]);

  // Type definitions
  using Simplex_tree = Gudhi::Simplex_tree<>;
  using Filtration_value = Simplex_tree::Filtration_value;
  using Rips_complex = Gudhi::rips_complex::Rips_complex<Filtration_value>;
  using Distance_matrix = std::vector<std::vector<Filtration_value>>;

  // ----------------------------------------------------------------------------
  // Init of a Rips complex from a distance matrix in a csv file
  // Default separator is ';'
  // ----------------------------------------------------------------------------
  Distance_matrix distances = Gudhi::read_lower_triangular_matrix_from_csv_file<Filtration_value>(csv_file_name);
  Rips_complex rips_complex_from_file(distances, threshold);

  std::streambuf* streambufffer;
  std::ofstream ouput_file_stream;

  if (argc == 5) {
    ouput_file_stream.open(std::string(argv[4]));
    streambufffer = ouput_file_stream.rdbuf();
  } else {
    streambufffer = std::cout.rdbuf();
  }

  Simplex_tree stree;
  rips_complex_from_file.create_complex(stree, dim_max);
  std::ostream output_stream(streambufffer);

  // ----------------------------------------------------------------------------
  // Display information about the Rips complex
  // ----------------------------------------------------------------------------
  output_stream << "Rips complex is of dimension " << stree.dimension() <<
                   " - " << stree.num_simplices() << " simplices - " <<
                   stree.num_vertices() << " vertices." << std::endl;

  output_stream << "Iterator on Rips complex simplices in the filtration order, with [filtration value]:" <<
                   std::endl;
  for (auto f_simplex : stree.filtration_simplex_range()) {
    output_stream << "   ( ";
    for (auto vertex : stree.simplex_vertex_range(f_simplex)) {
      output_stream << vertex << " ";
    }
    output_stream << ") -> " << "[" << stree.filtration(f_simplex) << "] ";
    output_stream << std::endl;
  }

  ouput_file_stream.close();
  return 0;
}

When launching:

$> ./Rips_complex_example_from_csv_distance_matrix ../../data/distance_matrix/full_square_distance_matrix.csv 1.0 3

the program output is:

Rips complex is of dimension 3 - 24 simplices - 7 vertices.
Iterator on Rips complex simplices in the filtration order, with [filtration value]:
   ( 0 ) -> [0] 
   ( 1 ) -> [0] 
   ( 2 ) -> [0] 
   ( 3 ) -> [0] 
   ( 4 ) -> [0] 
   ( 5 ) -> [0] 
   ( 6 ) -> [0] 
   ( 3 2 ) -> [5] 
   ( 5 4 ) -> [5.38516] 
   ( 2 0 ) -> [5.83095] 
   ( 1 0 ) -> [6.08276] 
   ( 3 1 ) -> [6.32456] 
   ( 2 1 ) -> [6.7082] 
   ( 2 1 0 ) -> [6.7082] 
   ( 3 2 1 ) -> [6.7082] 
   ( 6 5 ) -> [7.28011] 
   ( 4 2 ) -> [8.94427] 
   ( 3 0 ) -> [9.43398] 
   ( 3 1 0 ) -> [9.43398] 
   ( 3 2 0 ) -> [9.43398] 
   ( 3 2 1 0 ) -> [9.43398] 
   ( 6 4 ) -> [9.48683] 
   ( 6 5 4 ) -> [9.48683] 
   ( 6 3 ) -> [11] 

Copyright

GNU General Public License v3.

Contact: gudhi-users@lists.gforge.inria.fr